In an undirected graph, a cut vertex (or articulation point) is a vertex, and if we remove it, then the graph splits into two disconnected components. As an example, consider the following figure. Removal of the “D” vertex divides the graph into two connected components ({E,F} and {A,B, C, G}).
Similarly, removal of the “C” vertex divides the graph into ({G} and {A, B,D,E,F}). For this graph, D and C are the cut vertices.
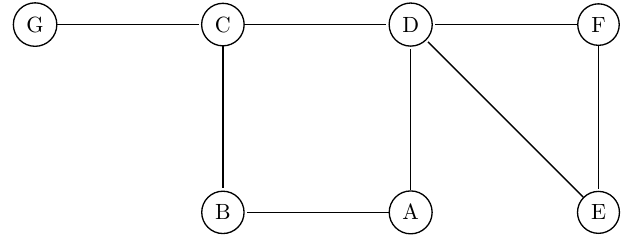
A connected, undirected graph is called bi – connected if the graph is still connected after removing any vertex.
DFS provides a linear-time algorithm (O(n)) to find all cut vertices in a connected graph. Starting at any vertex, call a DFS and number the nodes as they are visited. For each vertex v, we call this DFS number dfsnum(v). The tree generated with DFS traversal is called DFS spanning tree. Then, for every vertex v in the DFS spanning tree, we compute the lowest-numbered vertex, which we call low(v), that is reachable from v by taking zero or more tree edges and then possibly one back edge (in that order).
Based on the above discussion, we need the following information for this algorithm: the dfsnum of each vertex in the DFS tree (once it gets visited), and for each vertex v, the lowest depth of neighbors of all descendants of v in the DFS tree, called the low.
The dfsnum can be computed during DFS. The low of v can be computed after visiting all descendants of v (i.e., just before v gets popped off the DFS stack) as the minimum of the dfsnum of all neighbors of v (other than the parent of v in the DFS tree) and the low of all children of v in the DFS tree.
The root vertex is a cut vertex if and only if it has at least two children. A non-root vertex u is a cut vertex if and only if there is a son v of u such that low(v) ≥ dfsnum(u). This property can be tested once the DFS is returned from every child of u (that means, just before u gets popped off the DFS stack), and if true, u separates the graph into different bi-connected components. This can be represented by computing one bi-connected component out of every such v (a component which contains v will contain the sub-tree of v, plus u), and then erasing the sub-tree of v from the tree.
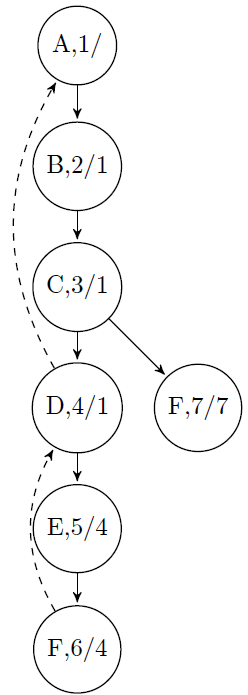
For the given graph, the DFS tree with dfsnum/low can be given as shown below:
Question 1: Write a function that return the cut vertices or articulation points.
Let G be a connected graph. An edge uv in G is called a bridge of G if G – uv is disconnected.
Consider the following graph:

If we remove the edge uv then the graph splits into two components. For this graph, uv is a bridge. The discussion we had for cut vertices holds good for bridges also.
The only change is, instead of printing the vertex, we give the edge. The main observation is that an edge (u, v) cannot be a bridge if it is part of a cycle. If (u, v) is not part of a cycle, then it is a bridge.
We can detect cycles in DFS by the presence of back edges, (u, v) is a bridge if and only if none of v or v’s children has a back edge to u or any of u’s ancestors. To detect whether any of v’s children has a back edge to u’s parent, we can use a similar idea as above to see what is the smallest dfsnum reachable from the subtree rooted at v.
Question 2: Write functions that return cut bridges and cut edges of a graph.
Difficulty level

This exercise is mostly suitable for students
#include<stdio.h>
#include<stdlib.h>
#define min(a,b) (((a) < (b)) ? (a) : (b))
typedef struct {
int V;
int E;
int **Adj; // since we need 2 dimensional matrix
} Graph;
Graph* adjacencyMatrix() {
int i, u, v;
Graph* G=(Graph*) malloc(sizeof(Graph));
printf("Enter the number of Vertices: ");
scanf("%d", &G->V);
printf("Enter the number of Edges: ");
scanf("%d", &G->E);
G->Adj = (int **)malloc(G->V * sizeof(int*));
for (u = 0; u < G->V; u++)
G->Adj[u] = (int *)malloc(G->V * sizeof(int));
for (u = 0; u<G->V; u++)
for (v = 0; v<G->V; v++)
G->Adj[u][v] = 0;
for (i = 0; i < G->E; i++) {
printf("Enter the edge: ");
scanf("%d %d", &u,&v);
// for undirected graph, set both
G->Adj[u][v] = 1;
G->Adj[v][u] = 1;
}
return G;
}
void DFSTraversal(Graph* G, int index, int Visited[]) {
int v;
printf("%d ",index);
for (v = 0; v < G->V; v++) {
if (!Visited[v] && G->Adj[index][v])
{
Visited[v]=1;
DFSTraversal(G, v, Visited);
}
}
}
void DFS(Graph *G) {
int i;
int *Visited;
Visited = (int *)malloc(G->V * sizeof(int));
for (i = 0; i < G->V; i++)
Visited[i] = 0;
// this loop is required if the graph has more than one component
for (i = 0; i < G ->V; i++)
if (!Visited[i])
{
Visited[i] = 1;
DFSTraversal(G, i, Visited);
}
}
void Cutvertices(Graph *G, int u, int dfsnum[], int low[], int *dfsNumberCounter, int dfsRoot, int *rootChildren, int articulationvertex[], int parent[])
{
int v;
low[u]=dfsnum[u]=(*dfsNumberCounter)++;
for (v = 0; v < G->V; v++)
{
if(G->Adj[u][v])
if(dfsnum[v]==-1)
{
parent[v]=u;
if(u == dfsRoot) (*rootChildren)++;
Cutvertices(G, v, dfsnum, low, dfsNumberCounter, dfsRoot, rootChildren, articulationvertex, parent);
if(low[v] >= dfsnum[u] )
articulationvertex[u]=1;
if(low[v] > dfsnum[u] )
printf(" -- Edge (%d %d) is a bridge\n",u, v);
low[u]=min(low[u],low[v]);
}
else if(v !=parent[u]) // (u,v) is a back edge
low[u]=min(low[u],dfsnum[v]);
}
}
void test() {
int *dfsnum, *low, dfsNumberCounter, i,
dfsRoot, rootChildren, *articulationvertex, *parent;
Graph *G = adjacencyMatrix();
dfsnum = (int *)malloc(G->V * sizeof(int));
low = (int *)malloc(G->V * sizeof(int));
parent = (int *)malloc(G->V * sizeof(int));
articulationvertex = (int *)malloc(G->V * sizeof(int));
for (i = 0; i < G->V; i++)
dfsnum[i]=-1 , parent[i]=low[i]=articulationvertex[i]=0;
dfsNumberCounter=0;
for (i = 0; i < G ->V; i++)
if (dfsnum[i]==-1)
{
dfsRoot = i;
rootChildren=0;
Cutvertices(G, i, dfsnum, low, &dfsNumberCounter, dfsRoot, &rootChildren, articulationvertex, parent);
articulationvertex[dfsRoot]=(rootChildren>1);
}
printf("Articulation Points:\n");
for (int i = 0; i < G ->V; i++)
if (articulationvertex[i])
printf(" Vertex %d\n", i);
}
int main()
{
test();
return 0;
}Back to the list of exercises
Looking for a more challenging exercise, try this one !!
 Kruskal Algorithm - Minimal Spanning Tree
Kruskal Algorithm - Minimal Spanning Tree