If the graph has negative edge costs, then Dijkstra's algorithm does not work.
The problem is that once a vertex $$u$$ is declared known, it is possible that from some other, unknown vertex $$v$$ there is a path back to $$u$$ that is very negative. In such a case, taking a path from $$s$$ to $$v$$ back to $$u$$ is better than going from $$s$$ to $$u$$ without using $$v$$.

A combination of Dijkstra's algorithm and unweighted algorithms will solve the problem.

Initialize the queue with $$s$$. Then, at each stage, we DeQueue a vertex $$v$$. We find all vertices $$W$$ adjacent to $$v$$ such that, distance to $$v + weight (v,w)$$ < old distance to $$w$$.

We update $$w$$ old distance and path, and place $$w$$ on a queue if it is not already there. A bit can be set for each vertex to indicate presence in the queue. We repeat the process until the queue is empty.

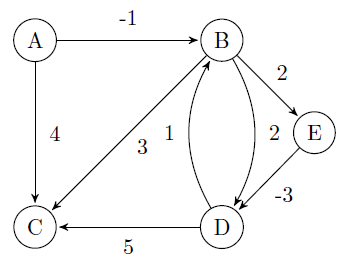
Example:
Bellman-Ford algorithm can be used to find the shortest path from source A to the remaining vertices in the graph.

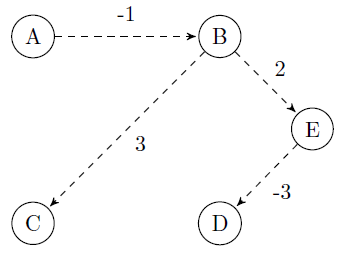
The final minimum cost tree which Bellman-Ford algorithm generates is:

Given the following declaration,
typedef struct {
    int V;
    int E;
    int **Adj;
} Graph;

1. Write a function that reads a graph containing negative weights.
2. Write a function that takes as parameters a weighted graph and an vertex, and returns the final minimum cost tree using Bellman-Ford algorithm.
3. Write a main function to test your function.

****************************************************
****************************************************

		USING ADJACENCY MATRIX

****************************************************
****************************************************

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<limits.h>
#define N 20

typedef int element;

typedef struct 
{
	element data[N]; /* queue content */
	int front, length;
} queue;



queue CreateQueue()
{
	queue q;
	q.front = 0; q.length=0;
	return q;
}
int isEmptyQueue(queue q)
{
	return q.length == 0;
}

int isFullQueue(queue q)
{
	return q.length ==N;
}

int EnQueue(queue *q, element e)
{
	if (isFullQueue(*q)) return 0;
	q->data[(q->front + q->length)%N] = e;
	q->length = q->length + 1;
	return 1;
}

int DeQueue(queue *q)
{
	if (isEmptyQueue(*q)) return 0;
	q->front=(q->front + 1) % N;
	q->length--;
	return 1;
}

int Front(queue q, element *e)
{
	if (isEmptyQueue(q)) return 0;
	*e = q.data[q.front];
	return 1;
}


typedef struct {
	int V;
	int E;
	int **Adj; // since we need 2 dimensional matrix
} Graph;

Graph* adjacencyMatrix() {
	int i, u, v, w;
	Graph* G = (Graph*)malloc(sizeof(Graph));
	printf("Enter the number of Vertices: ");
	scanf("%d", &G->V);
	printf("Enter the number of Edges: ");
	scanf("%d", &G->E);
	G->Adj = (int **)malloc(G->V * sizeof(int*));
	for (u = 0; u < G->V; u++)
		G->Adj[u] = (int *)malloc(G->V * sizeof(int));

	for (u = 0; u<G->V; u++)
		for (v = 0; v<G->V; v++)
			G->Adj[u][v] = 0;
	for (i = 0; i < G->E; i++) {
		printf("Enter the edge and the weight: ");
		scanf("%d %d %d", &u, &v, &w);
		G->Adj[u][v] = w;
	}
	return G;
}
 
void BellmanFord(Graph *G, int s) {
	queue q;
	int  i, v, w,dist;
	int *distance, *Path, *inqueue;

	q = CreateQueue();
	Path = (int *)malloc(G->V * sizeof(int));
	distance = (int *)malloc(G->V * sizeof(int));
	inqueue = (int *)malloc(G->V * sizeof(int));
	for (i = 0; i < G->V; i++)
	{ 
		distance[i] = INT_MAX;
		inqueue[i] = 0;
	}
	EnQueue(&q, s);
	distance[s] = 0;
	inqueue[s] = 1;

	while (Front(q, &v)) {
		inqueue[v]=0;
		DeQueue(&q);
		for (w = 0; w < G->V; w++)
			if (G->Adj[v][w] != 0) {
				dist = distance[v] + G->Adj[v][w];
				if (distance[w] >dist) {
					distance[w] = distance[v] + G->Adj[v][w];
					Path[w] = v;
					if(!inqueue[w])
					{
						inqueue[w]=1;
						EnQueue(&q, w);

					}
				}
			}
	}
	for (v = 0; v < G->V; v++)
		printf("%d should be reached from %d of total weight %d\n", v, Path[v], distance[v]);
}

void test() {
	int u, v;
	Graph *G = adjacencyMatrix();
	BellmanFord(G, 0);
}


int main()
{
	test();
	return 0;
}




****************************************************
****************************************************

		USING ADJACENCY LIST

****************************************************
****************************************************

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<limits.h>
#define N 20

typedef int element;

typedef struct 
{
	element data[N]; /* queue content */
	int front, length;
} queue;



queue CreateQueue()
{
	queue q;
	q.front = 0; q.length=0;
	return q;
}
int isEmptyQueue(queue q)
{
	return q.length == 0;
}

int isFullQueue(queue q)
{
	return q.length ==N;
}

int EnQueue(queue *q, element e)
{
	if (isFullQueue(*q)) return 0;
	q->data[(q->front + q->length)%N] = e;
	q->length = q->length + 1;
	return 1;
}

int DeQueue(queue *q)
{
	if (isEmptyQueue(*q)) return 0;
	q->front=(q->front + 1) % N;
	q->length--;
	return 1;
}

int Front(queue q, element *e)
{
	if (isEmptyQueue(q)) return 0;
	*e = q.data[q.front];
	return 1;
}


typedef struct node {
	int vertexNumber;
	int weight;
	struct node * next;
} node;

typedef struct {
	int V;
	int E;
	node** Adj;  //array of linked list
} Graph;

Graph* adjacencyList() {
	int i, x, y, w;
	node * temp, *temp2;
	Graph* G=(Graph*) malloc(sizeof(Graph));

	printf("Enter the number of Vertices: ");
	scanf("%d", &G->V);
	printf("Enter the number of Edges: ");
	scanf("%d", &G->E);
	G->Adj = (node **)malloc(G->V * sizeof(node));
	for (i = 0; i < G->V; i++) {
		G->Adj[i] = (node *)malloc(G->V * sizeof(node));
		G->Adj[i]->vertexNumber = i;
		G->Adj[i]->next = NULL;
	}
 
	for (i = 0; i < G->E; i++) {
		printf("Enter the edge and the weight: ");
		scanf("%d %d %d", &x,&y, &w);
		temp = (node*)malloc(sizeof(node));
		temp->vertexNumber = y;
		temp->weight = w;
        	temp->next = NULL;
        
		temp2 = G->Adj[x];
		while (temp2->next != NULL)
			temp2 = temp2->next;
		temp2->next = temp;
		
	}
	return G;
}
 
void BellmanFord(Graph *G, int s) {
	queue q;
	int  i, v, w,dist;
	int *distance, *Path, *inqueue;
	node * head;


	q = CreateQueue();
	Path = (int *)malloc(G->V * sizeof(int));
	distance = (int *)malloc(G->V * sizeof(int));
	inqueue = (int *)malloc(G->V * sizeof(int));

	for (i = 0; i < G->V; i++)
	{ 
		distance[i] = INT_MAX;
		inqueue[i] = 0;
	}
	EnQueue(&q, s);
	distance[s] = 0;
	inqueue[s] = 1;

	while (Front(q, &v)) {
		inqueue[v]=0;
		DeQueue(&q);
		head=G->Adj[v]->next;
		while(head)
	    	{
 
			dist = distance[v] + head->weight;
			if (distance[head->vertexNumber] >dist) {
				distance[head->vertexNumber] = distance[v] + head->weight;
				Path[head->vertexNumber] = v;
				if(!inqueue[head->vertexNumber])
				{
					inqueue[head->vertexNumber]=1;
					EnQueue(&q, head->vertexNumber);
				}
			}
			
			head = head->next;
		}
	}
	for (v = 0; v < G->V; v++)
		printf("%d should be reached from %d of total weight %d\n", v, Path[v], distance[v]);
}

void test() {
	int u, v;
	Graph *G = adjacencyList();
	BellmanFord(G, 0);
}


int main()
{
	test();
	return 0;
}