A historian wants to classify a set of events. Each event is characterized by a $$\textit{title}$$, a $$\textit{location}$$ and a $$\textit{period}$$ of time (as most of the events are spread over several years). $$\textit{Title}$$ and $$\textit{location}$$ are strings, while the $$\textit{period}$$ is a closed interval $$[start,end]$$, where $$start$$ and $$end$$ is a pair of integers such that $$-\infty < start \leq end <+\infty$$. 

In the following, we use the following declarations:

typedef struct {int start, end;} interval;
typedef struct {
     char *title, *location;
     interval period;} Event;

Here are some examples of events:

$$\begin{array}{|c|c|c|}
\hline \textbf{Title} & \textbf{Location} & \textbf{Period} \\
\hline \text{World War II} & world & [1939-1945] \\
\hline \text{First Atomic Bomb} & Hiroshima & [1945-1945] \\
\hline \text{JFK president} & USA & [1961-1963] \\
\hline \text{Independence} & Lebanon & [1943-1943] \\
\hline\end{array}$$

Note that certain events are spread over several years, while others begin and end the same year. 

In order to classify these events, the historian builds a binary tree of events ($$\texttt{BtreeE}$$) whose data are events such as:

• If $$EvL$$ is in the left subtree of $$Ev$$, then $$EvL.start \leq Ev.start$$
• If $$EvR$$ is in the right subtree of $$Ev$$, then $$EvR.start > Ev.start$$

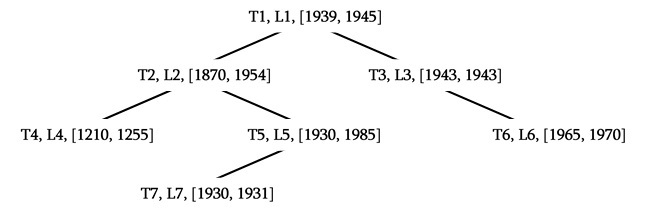
Thus, an event tree is a binary search tree for the event starting year in which repetitions can occur since $$\textbf{EvL.start} \leq \texttt{Ev.start}$$ (see figure below, where T$$_i$$ denotes a $$\textit{title}$$ and L$$_i$$ a $$\textit{location}$$). We therefore have the following declaration:

typedef struct node {
    Event data;
     struct node *Left, *Right;} *BtreeE;

• Write a recursive function $$\texttt{int contains(BtreeE B, int year)}$$ that returns the number of events of $$B$$ such as $$year$$ $$\in$$ interval of these events.
• Write an iterative function that returns the minimum interval that contains all the intervals of events of a given $$\texttt{BtreeE}$$.
  In the previous example, the result will be $$[1210, 1985]$$.
• Write a function $$\texttt{int isBtreeE(BtreeE B)}$$ that determines whether a given event tree $$\texttt{B}$$ satisfies the properties of a $$\texttt{BtreeE}$$.
• Write a function $$\texttt{int LongestInterval(BtreeE B, Event E)}$$ that returns the time in years from the largest inersection event between $$E$$ and those of $$B$$.
  Example: the intersection of the event T8, L8, [1923-1960] with the previous tree is 31; it comes from the intersection with T2, L2, [1870-1954].
• Write a function $$\texttt{int maxLong(BtreeE B)}$$ that returns the longest common period (intersection) of two events in a given $$\texttt{BtreeE}$$.
  In the previous tree, the events, T2,L2,[1870-1954] and T5,L5,[1930-1985] have an intersection of 24 years (between 1930 and 1954).

int contains (Btree B, int year)
{
	if(B==NULL)
		return 0;
	if( year >= B->data.period.start && year <= B->data.period.end )
		return 1+ contains (B->left,year)+contains (B->right,year);
	return contains (B->left,year)+contains (B->right,year);
}


int contains2(Btree B, interval *v)
{
	element e;
	int min = INT_MAX;
	int max = INT_MIN;
	if(B)
	{
		queue q = CreateQueue();
		EnQueue(&q,B);
		while(Front(q,&e))
		{
			DeQueue(&q);
			if(e->data.period.start<min)
				min=e->data.period.start;
			if(e->data.period.end>max)
				max=e->data.period.end;
			if(e->left)
				EnQueue(&q,e->left);
			if(e->right)
				EnQueue(&q,e->right);
		}
		v->start=min;
		v->end=max;
		return 1;
	}
	return 0;
}

int FindMin(Btree tree)
 {
	int res;
 	int lres, rres;
if (tree == NULL) return INT_MAX;
res = tree->data.period.start;
lres = FindMin(tree->left);
rres = FindMin(tree->right);
    	if (lres < res) 	res = lres;
    	if (rres < res)	res = rres;
   	return res;
 }

 int FindMax(Btree tree)
 {
	int res;
	int lres, rres;
    	if (tree == NULL)
      		return INT_MIN;
     	res = tree->data.period.start;
     	lres = FindMax(tree->left);
     	rres = FindMax(tree->right);
    	if (lres > res)	res = lres;
    	if (rres > res)	res = rres;
    	return res;
 }

int isBtreeE(Btree B)
{
	if(B == NULL)	 return 1;
	if(B->left != NULL && FindMax(B->left) > B->data.period.start)	 return 0;
	if(B->right != NULL && FindMin(B->right) <= B->data.period.start)	 return 0;
	if(!isBtreeE(B->left) || !isBtreeE(B->right))  return 0;
	 return 1;
}

 


int longestInterval(Btree B, Event E)
{
	element e;
	int interval = INT_MIN;
	int lower_bound,upper_bound;
	if(B)
	{
		queue q = CreateQueue();
		EnQueue(&q,B);
		while(Front(q,&e))
		{
			DeQueue(&q);
			lower_bound=max(E.period.start,e->data.period.start);
			upper_bound=min(E.period.end,e->data.period.end);
			if(lower_bound<=upper_bound && 
upper_bound-lower_bound>interval &&  
strcmp(e->data.title,E.title))
				interval=upper_bound-lower_bound; 
			if(e->left)
				EnQueue(&q,e->left);
			if(e->right)
				EnQueue(&q,e->right);
		}
		return interval;
	}
	return -1;
}

int maxLongr(Btree B, Btree tree)
{
	 
	int res, lres, rres;

if (tree == NULL) return INT_MIN;
	res = longestInterval(B, tree->data);
     	lres = maxLongr(B,tree->left);
     	rres = maxLongr(B,tree->right);
    	if (lres > res)      res = lres;
    	if (rres > res)      res = rres;
    	return res;
}

int maxLong(Btree B)
{
	return maxLongr(B,B );
}