A max-heap is a perfect binary tree in which data of each node is $$>$$ than those of its children (the root contains the max).

• Consider the following max-heap.
  
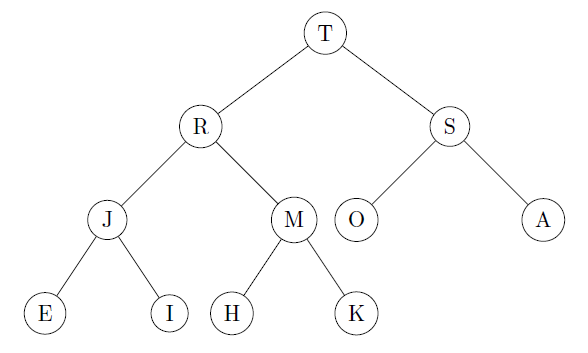
  The max-heap above resulted after a sequence of $$\texttt{insert}$$ and $$\texttt{delete-the-maximum}$$ operations. Assume that the last operation was an $$\texttt{insert}$$. Which key(s) could have been the one inserted last? Give all possibilities.

•  Draw the heap that results after deleting the maximum key from the heap above.

• A $$\texttt{delete-the-maximum}$$ operation in the binary heap at left results in the binary heap at right.

  

  
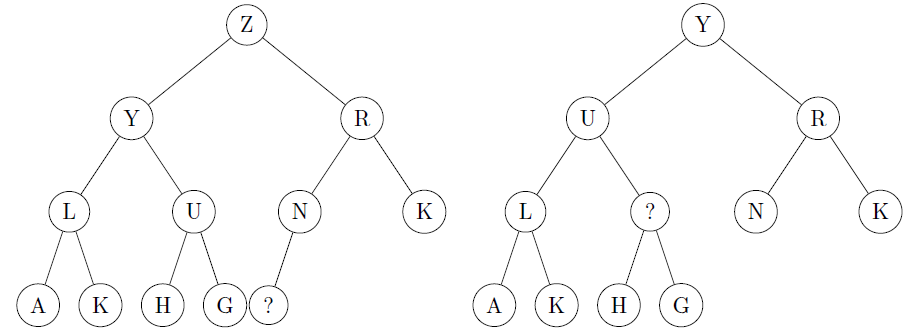
  Which of the 26 letters of the alphabet could be the one labeled with a question mark? Give all possibilities.

1.	  K M R
2.	 
                 S
        R                O
   J          M      K        A
E     I    H
 
3.	  I J K L M