Antoun J. Yaacoub Ph.D.

We would like in this question to arrange words of any length in a tree structure represented in levels as follows: each node $p$ of the tree of level $i$ has the following structure:

typedef char element;typedef struct node{ element data; struct node *left, *right, *nextlevel;} *tree;

All characters arranged in the left subtree are strictly less than $\texttt{data}$ .

All characters arranged in the right subtree are strictly greater than $\texttt{data}$ .

A word of the form: $C_1 C_2 \cdots C_n$ will be arranged as follows:
$C_1$ in the tree of level 1
$C_2$ in the tree of level 2 pointed by the $C_1$ node
$\cdots$
$C_i$ in the tree of level $i$ pointed by the $C_{i-1}$ node.

Example: After inserting the words: $\texttt{mn}$ , $\texttt{ke}$ , $\texttt{me}$ , $\texttt{r}$ , $\texttt{uf}$ , $\texttt{kn}$ , $\texttt{ub}$ , $\texttt{mz}$ , $\texttt{kd}$ , $\texttt{ubc}$ , $\texttt{ubz}$ , and $\texttt{ubb}$ , we get the following tree:

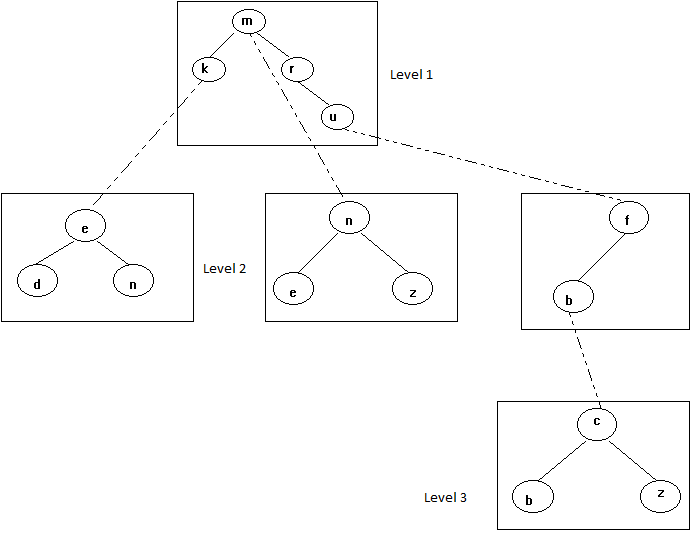
Write a recursive function that searches for a character $x$ in a tree $A$ and returns the address of the node containing the character $x$ , $\texttt{NULL}$ otherwise.
Write a recursive function that inserts a character $x$ into a tree $A$ and returns also the address of the newly created node.

Using the functions written above:

Write a function that determines the largest prefix (of maximum length) in the tree structure of a given word. (Example if $\texttt{word}$ = " $\texttt{ubt}$ ", the largest prefix that exists in the structure is " $\texttt{ub}$ ").
Your function should return the $\texttt{length}$ of the prefix and the $\texttt{address}$ of the last character of the prefix in the structure.
Deduct by writing the search function of a given $\texttt{word}$ from the prefix search.
Use the $\texttt{prefix}$ and $\texttt{insert}$ functions to insert a given word in the tree.

Difficulty level

Video recording

This exercise is mostly suitable for students

 tree find(tree A, element x)
{
	if (A == NULL)
		return NULL;
	else
		if (A->data == x)
			return A;
		else
			if (A->data > x)
				return find(A->left, x);
			return find(A->right,x);
}


int insert(element x, tree *A, tree *B)
{
	 
	if (*A == NULL)
	{
		*A = (tree)malloc(sizeof(struct node));
		if (!(*A)) return 0;
		(*A)->data = x;
		(*A)->left = (*A)->right = (*A)->nextlevel = NULL;
		*B = *A;
	}
	else
	{
		if (x == (*A)->data) return 0;
		if (x < (*A)->data)
			return insert(x, &((*A)->left), B);
		return insert(x, &((*A)->right), B);
	}
	return 1;
}


void prefix(tree S, element word[], int * length, tree *Address)
{
	int stop, i;
	tree R;

	stop = 0;
	i = 0;
	*Address = NULL;
	while (!stop)
	{
		R = find(S, word[i]);
		if (R == NULL)
			stop = 1;
		else
		{
			i++;
			*Address = R;
			S = R->nextlevel;
		}
	}
	*length = i;
}
 
int findword(tree S, element word[])
{
	int length;
	tree Address;
	prefix(S, word, &length, &Address);
	if (length == strlen(word))
		return 1;
	return 0;
}

int insertword(tree *S, element word[])
{
	int length;
	tree Address, adr, B;
	int j;

	prefix(*S, word, &length, &Address);
	if (length == strlen(word))
		printf("word exists");
	else
	{
		for (j = length ; j < strlen(word); j++)
		{
			if (Address != NULL)
				adr = Address->nextlevel;
			else
				adr = *S;
			if (!insert(word[j], &adr, &B)) return 0;
			if (*S == NULL)
				*S = adr;
			if (Address != NULL)
				if (Address->nextlevel != adr)
					Address->nextlevel = adr;
			Address = B;
		}
	}
	return 1;
}

Back to the list of exercises

Looking for a more challenging exercise, try this one !!

Kruskal Algorithm - Minimal Spanning Tree

Binary search trees in levels