Antoun J. Yaacoub Ph.D.

A famous solution for the shortest path problem was developed by Dijkstra. Dijkstra's algorithm is a generalization of the BFS algorithm. The regular BFS algorithm cannot solve the shortest path problem as it cannot guarantee that the vertex at the front of the queue is the vertex closest to source \(s\).

As in unweighted shortest path algorithm, here too we use the \(\texttt{Distance}\) table. The algorithm works by keeping the shortest distance of vertex \(v\) from the source in the \(\texttt{Distance}\) table. The value \(\texttt{Distance[v]}\) holds the distance from \(s\) to \(v\). The shortest distance of the source to itself is zero. The \(\texttt{Distance}\) table for all other vertices is set to -1 to indicate that those vertices are not already processed.

After the algorithm finishes, the \(\texttt{Distance}\) table will have the shortest distance from source \(s\) to each other vertex \(v\).

Notes:

Always pick the next closest vertex to the source.
It uses priority queue to store unvisited vertices by distance from s.
It does not work with negative weights.
To represent weights in the adjacency list, each vertex contains the weights of the edges (in addition to their identifier).
Instead of ordinary queue we use priority queue [distances are the priorities] and the vertex with the smallest distance is selected for processing.
The distance to a vertex is calculated by the sum of the weights of the edges on the path from the source to that vertex.
We update the distances in case the newly computed distance is smaller than the old distance which we have already computed.

Example:
Dijkstra's algorithm can be used to find the shortest path from source A to the remaining vertices in the graph.

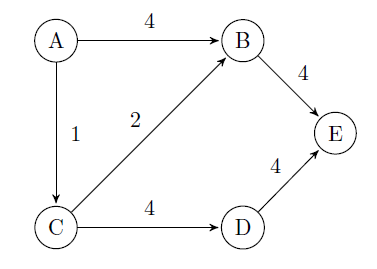
The above weighted graph has 5 vertices from A – E.

Initially the Distance table is:

\(\begin{array}{|c|c|c|}\hline \textbf{Vertex} & \textbf{Distance[v]} & \textbf{Vertex gaving Distance[v]}\\ \hline A & 0 & - \\ \hline B & -1& - \\ \hline C & -1 & - \\ \hline D & -1 & - \\ \hline E & -1 & - \\ \hline \end{array}\)

After the first step, from vertex A, we can reach B and C. So, in the Distance table we update the reachability of B and C with their costs.

\(\begin{array}{|c|c|c|}\hline \textbf{Vertex} & \textbf{Distance[v]} & \textbf{Vertex gaving Distance[v]}\\ \hline A & 0 & - \\ \hline B & 4& A \\ \hline C & 1 & A \\ \hline D & -1 & - \\ \hline E & -1 & - \\ \hline \end{array}\)

Now, let us select the minimum distance among all. The minimum distance vertex is C. That means, we have to reach other vertices from these two vertices (A and C). For example, B can be reached from A and also from C. In this case we have to select the one which gives the lowest cost. Since reaching B through C is giving the minimum cost (1 + 2), we update the Distance table for vertex B with cost 3 and the vertex from which we got this cost as C.

\(\begin{array}{|c|c|c|}\hline \textbf{Vertex} & \textbf{Distance[v]} & \textbf{Vertex gaving Distance[v]}\\ \hline A & 0 & - \\ \hline B & 3 & C \\ \hline C & 1 & A \\ \hline D & 5 & C \\ \hline E & -1 & - \\ \hline \end{array}\)

The only vertex remaining is E. To reach E, we have to see all the paths through which we can reach E and select the one which gives the minimum cost. We can see that if we use B as the intermediate vertex through C we get the minimum cost.

The final minimum cost tree which Dijkstra's algorithm generates is:

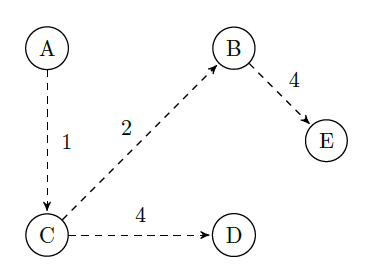
Given the following declaration,
typedef struct {
int V;
int E;
int **Adj;
} Graph;

Write a function that reads a weighted graph.
Write a function that takes as parameters a weighted graph and an vertex, and returns the final minimum cost tree using Dijkstra's algorithm.
Write a main function to test your function.

Difficulty level

Video recording

This exercise is mostly suitable for students

****************************************************
****************************************************

		USING ADJACENCY MATRIX

****************************************************
****************************************************

#include<stdio.h>
#include<stdlib.h>
#define N 20
typedef int element;
struct cell { 
	element data; 
	int priority;
	struct cell *next; 
};
 

typedef  struct { 
	struct cell *front; 
} queue;

typedef struct {
	int V;
	int E;
	int **Adj; // since we need 2 dimensional matrix
} Graph;


queue CreateQueue()
{
	queue q;
	q.front = NULL;
	return q;
}

int isEmptyQueue(queue q)
{
	return q.front == NULL;
}

int EnQueue(queue *q, element e, int priority)
{
	struct cell *temp, *href;
	temp = (struct cell *) malloc(sizeof(struct cell));
	if (!temp) return 0;
	temp->data = e;
	temp->priority = priority;
	if (q->front == NULL || priority < q->front->priority) {/*Queue is empty or item to be added has priority more than first item*/
		temp->next = q->front;
		q->front = temp;
	}
	else
	{
		href = q->front;
		while (href->next != NULL && href->next->priority <= priority)
			href = href->next;
		temp->next = href->next;
		href->next = temp;
	}

	return 1;
}

int DeQueue(queue *q)
{
	struct cell *temp;
	if (isEmptyQueue(*q)) return 0;
	temp = q->front;
	q->front = q->front->next;
	free(temp);
	return 1;
}

int Front(queue q, element *e)
{
	if (isEmptyQueue(q)) return 0;
	*e = q.front->data;
	return 1;
}

 

void display_queue(queue tmp)
{
	struct cell *temp = tmp.front;

	if (temp == NULL)
		printf("Queue is empty\n");
	else
	{
		printf("Queue is :\n");
		printf("Item\n");
		while (temp != NULL)
		{
			printf("%5d         %5d\n\n", temp->priority, temp->data);
			temp = temp->next;
		}
	}
}
void delete_head(struct cell **nodeRef)
{
	struct cell *p;
	p = *nodeRef;
	*nodeRef = (*nodeRef)->next;
	free(p);
}

// delete a given element (recursive)
int delete_value(struct cell **nodeRef, element e)
{
	if (*nodeRef == NULL)
		return 0;
	if ((*nodeRef)->data == e)
	{
		delete_head(nodeRef);
		return 1;
	}
	return delete_value(&((*nodeRef)->next), e);
}


void recursive_ordered_insert(struct cell **node, element value, int priority)
{
	struct cell *temp;
	if ((*node == NULL) || !((*node)->priority < priority))
	{
		temp = *node;
		*node = (struct cell *) malloc(sizeof(struct cell));
		if (!*node) return ;
		(*node)->data = value;
		(*node)->priority = priority;
		(*node)->next = temp;
		return;
	}

	 recursive_ordered_insert(&((*node)->next), value, priority);

}


void update_priority(queue *q, element data, int priority) {
	if (delete_value(&(q->front), data) == 1)
		recursive_ordered_insert(&(q->front), data, priority);
}



Graph* adjacencyMatrix() {
	int i, u, v, w;
	Graph* G = (Graph*)malloc(sizeof(Graph));
	printf("Enter the number of Vertices: ");
	scanf("%d", &G->V);
	printf("Enter the number of Edges: ");
	scanf("%d", &G->E);
	G->Adj = (int **)malloc(G->V * sizeof(int*));
	for (u = 0; u < G->V; u++)
		G->Adj[u] = (int *)malloc(G->V * sizeof(int));

	for (u = 0; u<G->V; u++)
		for (v = 0; v<G->V; v++)
			G->Adj[u][v] = 0;
	for (i = 0; i < G->E; i++) {
		printf("Enter the edge and the weight: ");
		scanf("%d %d %d", &u, &v, &w);
		G->Adj[u][v] = w;
	}
	return G;
}

void Dijkstra(Graph *G, int s) {
	queue q;
	int i,v, w, dist;
	int *distance, *Path;

	q = CreateQueue();
	Path = (int *)malloc(G->V * sizeof(int));
	distance = (int *)malloc(G->V * sizeof(int));
	for (i = 0; i < G->V; i++)
		distance[i] = -1;

	EnQueue(&q, s,0);
	distance[s] = 0;
	while (Front(q, &v)) {
		DeQueue(&q);
		for (w = 0; w < G->V; w++) 
			if (G->Adj[v][w] != 0) {
				dist = distance[v]+ G->Adj[v][w];
				if (distance[w] == -1) {
					distance[w] = dist;
					EnQueue(&q, w, dist);
					Path[w] = v;
				}
				else
					if (distance[w] > dist) {
						distance[w] = dist;
						update_priority(&q, w, dist);
						Path[w] = v;
					}

			}
		
			
	}
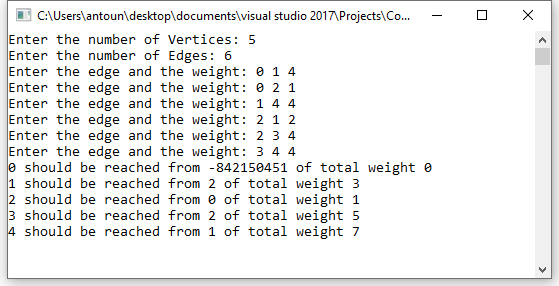
	for (v = 0; v < G->V; v++)
		printf("%d should be reached from %d of total weight %d\n", v, Path[v], distance[v]);
}

int test() {
	int u, v;
	Graph *G = adjacencyMatrix();
	Dijkstra(G, 0);
}


int main()
{
	test();
	return 0;
}




****************************************************
****************************************************

		USING ADJACENCY LIST

****************************************************
****************************************************

#include<stdio.h>
#include<stdlib.h>
#define N 20
typedef int element;
struct cell { 
	element data; 
	int priority;
	struct cell *next; 
};

typedef  struct { 
	struct cell *front; 
} queue;

 

queue CreateQueue()
{
	queue q;
	q.front = NULL;
	return q;
}

int isEmptyQueue(queue q)
{
	return q.front == NULL;
}

int EnQueue(queue *q, element e, int priority)
{
	struct cell *temp, *href;
	temp = (struct cell *) malloc(sizeof(struct cell));
	if (!temp) return 0;
	temp->data = e;
	temp->priority = priority;
	if (q->front == NULL || priority < q->front->priority) {/*Queue is empty or item to be added has priority more than first item*/
		temp->next = q->front;
		q->front = temp;
	}
	else
	{
		href = q->front;
		while (href->next != NULL && href->next->priority <= priority)
			href = href->next;
		temp->next = href->next;
		href->next = temp;
	}

	return 1;
}

int DeQueue(queue *q)
{
	struct cell *temp;
	if (isEmptyQueue(*q)) return 0;
	temp = q->front;
	q->front = q->front->next;
	free(temp);
	return 1;
}

int Front(queue q, element *e)
{
	if (isEmptyQueue(q)) return 0;
	*e = q.front->data;
	return 1;
}

 

void display_queue(queue tmp)
{
	struct cell *temp = tmp.front;

	if (temp == NULL)
		printf("Queue is empty\n");
	else
	{
		printf("Queue is :\n");
		printf("Item\n");
		while (temp != NULL)
		{
			printf("%5d         %5d\n\n", temp->priority, temp->data);
			temp = temp->next;
		}
	}
}
void delete_head(struct cell **nodeRef)
{
	struct cell *p;
	p = *nodeRef;
	*nodeRef = (*nodeRef)->next;
	free(p);
}

// delete a given element (recursive)
int delete_value(struct cell **nodeRef, element e)
{
	if (*nodeRef == NULL)
		return 0;
	if ((*nodeRef)->data == e)
	{
		delete_head(nodeRef);
		return 1;
	}
	return delete_value(&((*nodeRef)->next), e);
}


void recursive_ordered_insert(struct cell **node, element value, int priority)
{
	struct cell *temp;
	if ((*node == NULL) || !((*node)->priority < priority))
	{
		temp = *node;
		*node = (struct cell *) malloc(sizeof(struct cell));
		if (!*node) return ;
		(*node)->data = value;
		(*node)->priority = priority;
		(*node)->next = temp;
		return;
	}

	 recursive_ordered_insert(&((*node)->next), value, priority);

}


void update_priority(queue *q, element data, int priority) {
	if (delete_value(&(q->front), data) == 1)
		recursive_ordered_insert(&(q->front), data, priority);
}



typedef struct node {
	int vertexNumber;
	int weight;
	struct node * next;
} node;

typedef struct {
	int V;
	int E;
	node** Adj;  //array of linked list
} Graph;

Graph* adjacencyList() {
	int i, x, y, w;
	node * temp, *temp2;
	Graph* G=(Graph*) malloc(sizeof(Graph));

	printf("Enter the number of Vertices: ");
	scanf("%d", &G->V);
	printf("Enter the number of Edges: ");
	scanf("%d", &G->E);
	G->Adj = (node **)malloc(G->V * sizeof(node));
	for (i = 0; i < G->V; i++) {
		G->Adj[i] = (node *)malloc(G->V * sizeof(node));
		G->Adj[i]->vertexNumber = i;
		G->Adj[i]->next = NULL;
	}
 
	for (i = 0; i < G->E; i++) {
		printf("Enter the edge and the weight: ");
		scanf("%d %d %d", &x,&y, &w);
		temp = (node*)malloc(sizeof(node));
		temp->vertexNumber = y;
		temp->weight = w;
        	temp->next = NULL;
        
		temp2 = G->Adj[x];
		while (temp2->next != NULL)
			temp2 = temp2->next;
		temp2->next = temp;
		
	}
	return G;
}

void Dijkstra(Graph *G, int s) {
	queue q;
	int i,v, w, dist;
	int *distance, *Path;
	node * head;

	q = CreateQueue();
	EnQueue(&q, s,0);
	Path = (int *)malloc(G->V * sizeof(int));
	distance = (int *)malloc(G->V * sizeof(int));
	for (i = 0; i < G->V; i++)
		distance[i] = -1;

	distance[s] = 0;
	while (Front(q, &v)) {
		DeQueue(&q);
		head=G->Adj[v]->next;
		while(head)
	    	{
			dist = distance[v]+ head->weight;
			if (distance[head->vertexNumber] == -1) {
				distance[head->vertexNumber] = dist;
				EnQueue(&q, head->vertexNumber, dist);
				Path[head->vertexNumber] = v;
			}
			else
				if (distance[head->vertexNumber] > dist) {
					distance[head->vertexNumber] = dist;
					update_priority(&q, head->vertexNumber, dist);
					Path[head->vertexNumber] = v;
				}
			
			head = head->next;
		}
		
			
	}
	for (v = 0; v < G->V; v++)
		printf("%d should be reached from %d of total weight %d\n", v, Path[v], distance[v]);
}

int test() {
	int u, v;
	Graph *G = adjacencyList();
	Dijkstra(G, 0);
}


int main()
{
	test();
	return 0;
}

Back to the list of exercises

Looking for a more challenging exercise, try this one !!

Length of the longest ascending sequence of characters

Select your ad blocker:

Disable AdBlock:

Disable AdBlock Plus:

Disable Adguard AdBlocker:

Disable uBlock Origin:

Dijkstra Algorithm