We are interested to perform the dot product for unequal-length vectors.

Algebraically, the dot product is the sum of the products of the corresponding entries of the two sequences of numbers.

The dot product of two unequal-length vectors $A = [a_0, a_1, \cdots, a_{N-1}]$ and $B = [b_0, b_1, \cdots, b_{M-1}]$, where $N>0$, $0<M<N$ and $N = k\times M, k \in \mathbb{N}-\{0\}$, is defined as: $A \cdot B = a_0b_0 + \cdots + a_kb_{M-1} + a_{k+1}b_0 + \cdots + a_{N-1}b_{M-1}$.

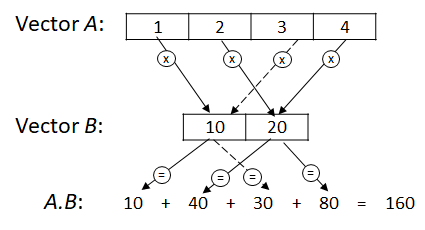
Running examples

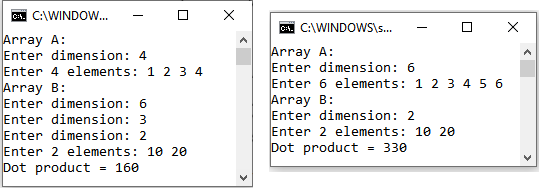
• Write the function $\texttt{int READDIM_A()}$ that reads and returns a strictly positive integer $N$ less than 50;
• Write the function $\texttt{int READDIM_B(int N)}$ that reads and returns a strictly positive integer $M$ divisible by $N$;
• Write the function $\texttt{void READARRAY(int Arr[], int C)}$ that reads $\texttt{C}$ positive integers of the array $\texttt{Arr}$;
• Write the function $\texttt{int DOTPRODUCT(int A[], int N, int B[], int M)}$ that returns the dot product of two unequal-length arrays;
• Using all the above written functions, write a $\texttt{main}$ function that reads two unequal-length arrays and then displays their dot product.

#include<stdio.h>
#define size 50

int READDIM_A()
{
	int N; 
	do {
		printf("Enter dimension: ");
		scanf("%d", &N);
	} while (N <= 0 || N>size);
	return N;
}

int READDIM_B(int N)
{
	int M;
	do {
		printf("Enter dimension: ");
		scanf("%d", &M);
	} while (M <= 0 || M > N || N % M);
	return M;
}

void READARRAY(int Arr[], int C)
{
	int i;
	printf("Enter %d elements: ", C);
	for (i = 0; i < C; i++)
		scanf("%d", &Arr[i]);
}


int DOTPRODUCT(int A[], int N, int B[], int M)
{
	int i, j, sum = 0;
	for (i = 0, j = 0; i < N; i++, j++)
		sum += A[i] * B[j%M];
	return sum;
}

int main()
{
	int A[size], B[size];
	int N, M; 

	printf("Array A:\n");
	N = READDIM_A();
	READARRAY(A, N);

	printf("Array B:\n");
	M = READDIM_B(N);
	READARRAY(B, M);

	printf("Dot product = %d\n", DOTPRODUCT(A,N,B,M));

	return 0;
}