Antoun J. Yaacoub Ph.D.

One application of trees is to game playing by computer. We illustrate this application by writing a C program to determine the "best" move in tic-tac-toe from a given board position.

Assume that there is a function evaluate that accepts a board position and an indication of a player (X or O) and returns a numerical value that represents how "good" the position seems to be for that player (the larger the value returned by evaluate, the better the position). Of course, a winning position yields the largest possible value, and a losing position yields the smallest. An example of such an evaluation function for tic-tac-toe is the number of rows, columns, and diagonals remaining open for one player minus the number remaining open for his or her opponent (except that the value 9 would be returned for a position that wins, and -9 for a position that loses). This function does not "look ahead" to consider any possible board positions that might result from the current position; it merely evaluates a static board position.

Given a board position, the best next move could be determined by considering all possible moves and resulting positions. The move selected should be the one that results in the board position with the highest evaluation. Such an analysis, however, does not necessarily yield the best move. Figure 1 illustrates a position and the five possible moves that X can make from that position. Applying the evaluation function just described to the five resulting positions yields the values shown. Four moves yield the same maximum evaluation, although three of them are distinctly inferior to the fourth. (The fourth position yields a certain victory for X, whereas the other three can be drawn by O.) In fact, the move that yields the smallest evaluation is as good or better than the moves that yield a higher evaluation. The static evaluation function, therefore, is not good enough to predict the outcome of the game. A better evaluation function could easily be produced for the game of tic-tac-toe (even if it were by the brute-force method of listing all positions and the appropriate response), but most games are too complex for static evaluators to determine the best response.

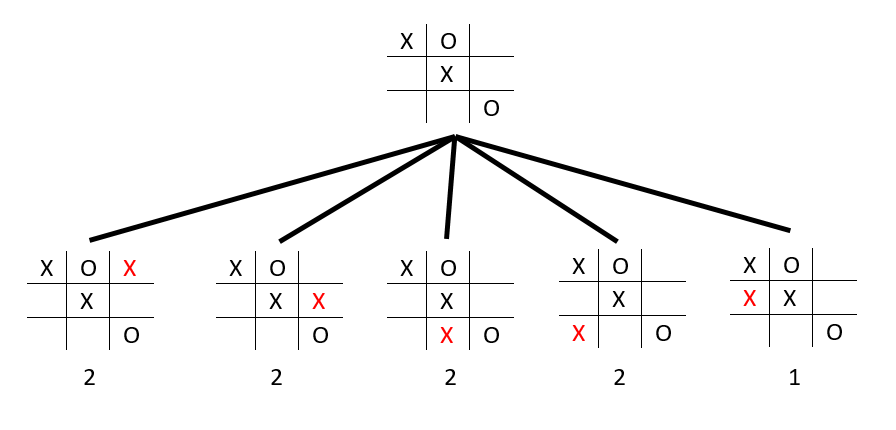
Figure 1: A position and the five possible moves that X can make from that position

Suppose that it were possible to look ahead several moves. Then the choice or a move could be improved considerably. Define the look ahead level as the number of future moves to be considered. Starting at any position, it is possible to construct a tree of the possible board positions that may result from each move. Such a tree is called a game tree. The game tree for the opening tic-tac-toe position with a look-ahead level of 2 is illustrated in Figure 2. (Actually other positions do exist, but because of symmetry considerations these are effectively the same as the positions shown.) Note that the maximum level (called the depth) of the nodes in such a tree is equal to the look-ahead level.

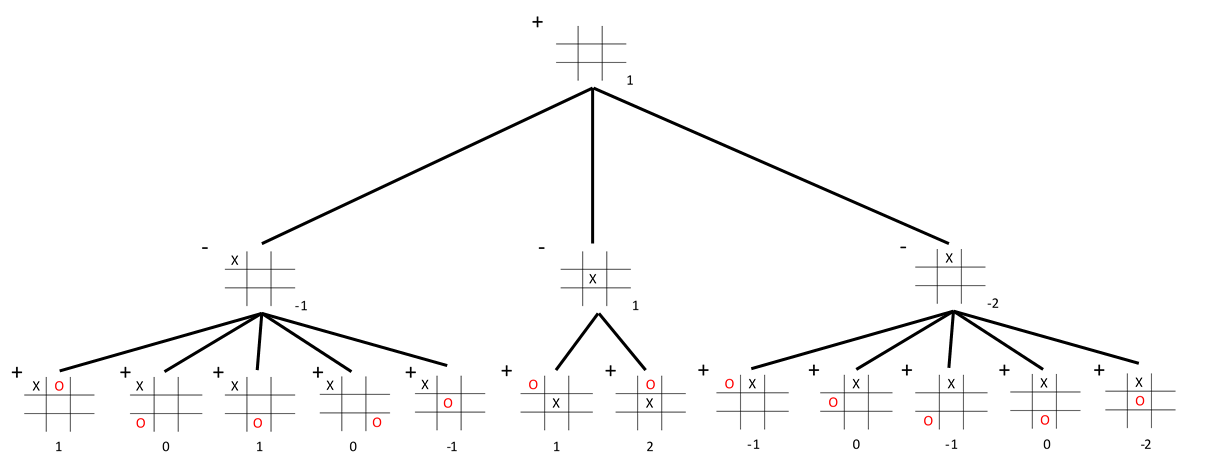
Figure 2 – A game tree for tic-tac-toe

Let us designate the player who must move at the root’s game position as plus and his or her opponent as minus. We attempt to find the best move for plus from the root’s game position. The remaining nodes of the tree may be designated as plus nodes or minus nodes, depending upon which player must move from that node’s position. Each node of Figure 2 is marked as a plus or as a minus node.

Suppose that the game positions of all the sons of a plus node have been evaluated for player plus. Then

clearly, plus should choose the move that yields the maximum evaluation. Thus, the value of a plus node to player plus is the maximum of the values of its sons. On the other hand, once plus has moved, minus will select the move that yields the minimum evaluation for player plus. Thus the value of a minus node to player plus is the minimum of the values of its sons.

Therefore, to decide the best move for player plus from the root, the positions in the leaves must be evaluated for player plus using a static evaluation function. These values are then moved up the game tree by assigning to each plus node the maximum of its sons’ values and to each minus node the minimum of its sons’ values, on the assumption that minus will select the move that is worst for plus. The value assigned to each node of Figure 2 by this process is indicated in that figure immediately below the node.

The move that plus should select, given the board position in the root node, is the one that maximizes its

value. Thus the opening move for X should be the middle square, as illustrated in Figure 2. Figure 3 illustrates the determination of O’s best reply. Note that the designation of "plus" and "minus" depends on whose move is being calculated. Thus, in Figure 2, X is designated as plus, whereas in Figure 3, O is designated as plus.

In applying the static evaluation function to a board position, the value of the position to whichever player is designated as plus is computed. This method is called the minimax method, since, as the tree is climbed, the maximum and minimum functions are applied alternately.

The best move for a player from a given position may be determined by first constructing the game tree

and applying a static evaluation function to the leaves. These values are then moved up the tree by applying the minimum and maximum at minus and plus nodes, respectively. Each node of the game tree must include a representation of the board and an indication of whether the node is a plus node or a minus node. Nodes may therefore be declared by

struct node type{
char board[3][3];
int turn;
struct node type *son;
struct node type *next;
};
typedef struct node type *NODEPTR;

p− > board[i][j] has the value ’X’, ’O’, or ’ ’ , depending on whether the square in row i and column j of that node is occupied by either of the players or is unoccupied.

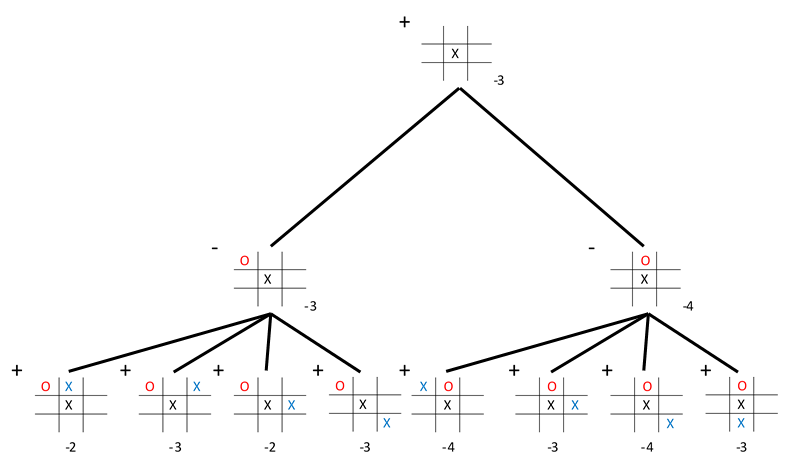
Figure 3 – Computing O’s reply

p− > turn has the value +1 or -1, depending on whether the node is a plus or minus node, respectively.

The remaining two fields of a node are used to position the node within the tree. p− > son points to the oldest son of the node and p− > next points to its next younger brother. We assume that the foregoing declaration is global that an available list of nodes has been established, and that appropriate getnode and freenode routines have been written.

The C function nextmove(brd, player, looklevel, newbrd) computes the best next move. brd is a 3-by-3 array representing the current board position, player is ’X’ or ’O’, depending on whose move is being computed (note that in tic-tac-toe the value of player could be computed from brd, so that this parameter is not strictly necessary), and looklevel is the look-ahead level used in constructing the tree. newbrd is an output parameter that represents the best board position that can be achieved by player from position brd. nextmove uses two auxiliary routines, buildtree and bestbranch. The function buildtree builds the game tree and returns a pointer to its root. The function bestbranch computes the value of two output parameters : best, which is a pointer to the tree node representing the best move, and value, which is the evaluation of that move using the minimax technique.

void nextmove(charbrd[][3], int looklevel, char player, char newbrd[][3])
{
NODEPTR ptree, best;
int i, j, value;
ptree=buildtree(brd,looklevel);
bestbranch(ptree,player,&best,&value);
for(i=0;i<3;i++)
for(j=0;j<3;j++)
newbrd[i][j]=best−>board[i][j];
}/*end nextmove*/

The function buildtree returns a pointer to the root of a game tree. It uses the auxiliary function getnode, which allocates storage for a node and returns a pointer to it. It also uses a routine expand(p, plevel, depth), in which p is a pointer to a node in a game tree, plevel is its level, and depth is the depth of the game tree that is to be constructed. expand produces the subtree rooted at p to the proper depth.

NODEPTR buildtree(char brd[][3], int looklevel)
{
NODEPTR ptree;
int i, j;
/*create the root of the tree and initialize it*/
ptree=getnode();
for(i=0;i<3;++i)
for(j=0;j<3;++j)
ptree−>board[i][j]=brd[i][j];
/*the root is a plus node by definition*/
ptree−>turn=1;
ptree−>son=NULL;
ptree−>next=NULL;
/*create the rest of the game tree*/
expand(ptree,0,looklevel);
return(ptree);
}/*end buildtree*/

expand may be implemented by generating all board positions that may be obtained from the board position pointed to by p and establishing them as the sons of p in the game tree. expand then calls itself recursively using these sons as parameters until the desired depth is reached. expand uses an auxiliary function generate, which accepts a board position brd and returns a pointer to a list of nodes containing the board positions that can be obtained from brd. This list is linked together by the next field. We leave the coding of generate as an exercise.

void expand(NODEPTR p, int plevel, int depth)
{
NODEPTR q;
if(plevel<depth)
{
   /*p is not at the maximum level*/
   q=generate(p−>board);
   p−>son=q;
   while(q!=NULL)
   {
      /*traverse the list of nodes*
      if(p−>turn==1)
         q−>turn=−1;
      else
         q−>turn=1;
      q−>son=NULL;
      expand(q,plevel+1,depth);
      q=q−>next;
   }/*end while*/
}/*end if*/
}/*end expand*/

Once the game tree has been created, bestbranch evaluates the nodes of the tree. When a pointer to a leaf is passed to bestbranch, it calls a function evaluate that statically evaluates the board position of that leaf for the player whose move we are determining. The coding of evaluate is left as an exercise. When a pointer to a nonleaf is passed to bestbranch, the routine calls itself recursively on each of its sons and then assigns the maximum of its sons’ to the nonleaf if it is a plus node, and the minimum if it is a minus node. bestbranch also keeps track of which son yielded this minimum or maximum value.

If p->turn is -1, the node pointed to by p is a minus node and it is to be assigned the minimum of the values assigned to its sons. If, however p->turn is + 1, the node pointed to by p is a plus node and its value should be the maximum of the values assigned to the sons of the node. If min(x,y) is the minimum ot x and y, and max(x,y) is their maximum, min(x,y) =-max(-x,-y) (you are invited to prove this as a trivial exercise). Thus, the correct maximum or minimum can be found as follows : in the case of a plus node, compute the maximum; in the case of a minus node, compute the maximum of the negatives of the values and then reverse the sign of the result. These ideas are incorporated into bestbranch. The output parameters *pbest and *pvalue are, respectively, a pointer to that son of the tree’s root that maximizes its value and the value of that son that has now been assigned to the root.

void bestbranch (NODEPTR pnd , char player , NODEPTR * pbest , int * pvalue )
{
NODEPTR p , pbest2 ;
int val ;
if(pnd−>son ==NULL)
{
   /* pnd is a leaf */
   *pvalue = evaluate(pnd−>board , player) ;
   *pbest = pnd ;
}
else
{
   /* the node is not a leaf, traverse the list of sons */
   p = pnd−>son ;
   bestbranch (p , player , pbest , pvalue ) ;
   *pbest = p ;
   if(pnd.turn == −1)
      *pvalue=−*pvalue ;
   p = p−>next ;
   while(p != NULL)
   {
      bestbranch (p , player , &pbest2 , &val ) ;
      if(pnd−>turn == −1)
         val = −val ;
      if( val > *pvalue )
      {
         *pvalue =val ;
         *pbest = p ;
      } /* end if*/
      p = p−>next ;
   } /*end while */
   if(pnd−>turn == −1)
      *pvalue = −*pvalue ;
} /* end if */
} /* end bestbranch */

Examine the routines of this section and determine whether all the parameters are actually necessary.
How would you revise the parameter lists ?
Write the routines generate and evaluate as described in the text.
Rewrite the programs under the implementation in which each tree node includes a field father containing a pointer to its father. Under which implementation are they more efficient ?
Write nonrecursive versions of the routines expand and bestbranch given in the text.
Modify the routine bestbranch in the text so that the nodes of the tree are freed after they are no longer needed.
Combine the processes of building the game tree and evaluating its nodes into a single process so that the entire game tree need not exist at any one time and nodes are freed when no longer necessary.
Modify the program of the previous exercise so that if the evaluation of a minus node is greater than the minimum of the values of its father’s older brothers, the program does not bother expanding that minus node’s younger brothers, and if the evaluation of a plus node is less than the maximum of the values of its father’s older brothers, the program does not bother expanding that plus node’s younger brothers.
This method is called the alpha-beta minimax method. Explain why it is correct.

Difficulty level

This exercise is mostly suitable for students

ï»¿#include <stdlib.h>
#include <stdio.h>
#include <string.h>
#include<conio.h>
#include "Btree.h"


/* This function counts the number of nodes in a binary tree */
int countNodes(Btree root)
{
	if (root == NULL)
		return 0;
	return (1 + countNodes(root->left) + countNodes(root->right));
}

/* This function checks if the binary tree is complete or not */
int isCompleteUtil(Btree root,  int index, int number_nodes)
{
	// An empty tree is complete
	if (root == NULL)
		return 1;

	// If index assigned to current node is more than
	// number of nodes in tree, then tree is not complete
	if (index >= number_nodes)
		return 0;

	// Recur for left and right subtrees
	return (isCompleteUtil(root->left, 2 * index + 1, number_nodes) &&
		isCompleteUtil(root->right, 2 * index + 2, number_nodes));
}

// This Function checks the heap property in the tree.
int isHeapUtil(Btree root)
{
	//  Base case : single node satisfies property
	if (root->left == NULL && root->right == NULL)
		return 1;

	//  node will be in second last level
	if (root->right == NULL)
	{
		//  check heap property at Node
		//  No recursive call , because no need to check last level
		return (root->data >= root->left->data);
	}
	else
	{
		//  Check heap property at Node and
		//  Recursive check heap property at left and right subtree
		if (root->data >= root->left->data &&
			root->data >= root->right->data)
			return ((isHeapUtil(root->left)) &&
			(isHeapUtil(root->right)));
		else
			return 0;
	}
}

//  Function to check binary tree is a Heap or Not.
int isHeap(Btree root)
{
	// These two are used in isCompleteUtil()
	unsigned int node_count = countNodes(root);
	unsigned int index = 0;

	if (isCompleteUtil(root, index, node_count) && isHeapUtil(root))
		return 1;
	return 0;
}


void main()
{

	Btree B = Construct(10,
		Construct(8,
			Construct(6,
				NULL,
				NULL),
			Construct(5,
				NULL,
				NULL)),
		Construct(9,
			Construct(2,
				NULL,
				NULL),
			Construct(-2,
				NULL,
				NULL)));

	if (isHeap(B))
		printf("Given binary tree is a Heap\n");
	else
		printf("Given binary tree is not a Heap\n");

	getch();
}

Back to the list of exercises

Looking for a more challenging exercise, try this one !!

Sorting using merge-sort algorithm

Game trees