An integer number is represented by a heap consisting of the number prime factors. 
Ex: the number 24 is represented by the heap below:

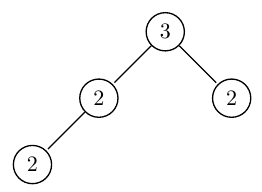
• Given the function $$\texttt{void primeFactors(int n)}$$ that prints the prime factors of an integer $$\texttt{n}$$, reuse its code to write a function that decomposes a given integer number into its prime factors and returns the corresponding heap.
• Write a function that, given a heap, returns the corresponding integer number;
• Write a function that computes the GCD of 2 numbers represented by 2 heaps.

// A function to print all prime factors of a given number n
void primeFactors(int n)
{
     int i;
     // Print the number of 2s that divide n
     while (n%2 == 0)
     {
          printf("%d ", 2);
          n = n/2;
     }

     // n must be odd at this point. So we can skip one element (Note i = i +2)
     for ( i = 3; i <= sqrt(n); i = i+2)
     {
          // While i divides n, print i and divide n
          while (n%i == 0)
          {
               printf("%d ", i);
               n = n/i;
          }
     }

     // This condition is to handle the case whien n is a prime number
     // greater than 2
     if (n > 2)
          printf ("%d ", n);
}

Heap PrimeFactors(int nb)
{
	int i;
	Heap h = CreateHeap(1,1);	

    	while (nb%2 == 0)
    	{
		Insert(&h,2);
        	nb = nb/2;
    	}

    	for ( i = 3; i <= sqrt(nb); i = i+2)
    	{
        	while (nb%i == 0)
        	{
            	Insert(&h,i);
            	nb = nb/i;
        	}
    	}
 
    	if (nb > 2)
        	Insert(&h,nb);
	return h;
}

int get_integer(Heap h)
{
	int i, nb;
	nb=h->array[0];
	for(i=1;i<h->count;i++)
		nb=nb*h->array[i];
	return nb;
}

int belong(int n, Heap h)
{
	int i;
	for(i=0;i<h->count;i++)
		if(n==h->array[i])
			return 1;
	return 0;
}

int GCD(Heap L, Heap R)
{
	int i,nb=1;
	for(i=0;i<L->count;i++)
	{
		if(belong(L->array[i],R))
			nb=nb*L->array[i];

	}
	return nb;
}


int GCDV2(Heap L, Heap R)
{
	int GCD=1;
	while(L->count && R->count)
	{
		if(L->array[0]==R->array[0])
		{
			GCD*=L->array[0];
			DeleteMax(&L);
			DeleteMax(&R);
		}
		else
			if(L->array[0]>R->array[0])
				DeleteMax(&L);
			else
				DeleteMax(&R);
	}
	return GCD;
}