We can keep two stacks within a single linear array so that neither of both stacks overflow until all of memory is used and an entire stack is never shifted to a different location within the array.
Thus, both stacks grow towards each other.

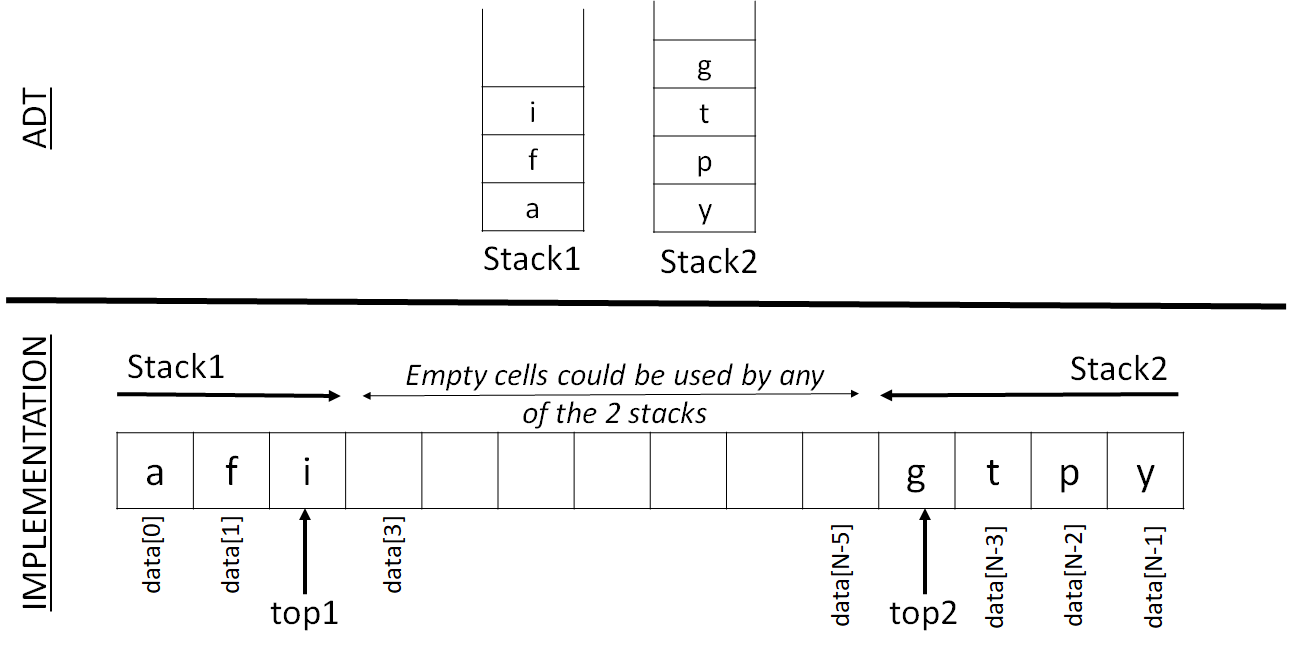
To design this, we can use the following declaration:
#define N 100
typedef ... element;
typedef struct{
     element data[N];
     int top1, top2;
} twoStacks;

The functions: \(\texttt{Push}\), \(\texttt{Pop}\), \(\texttt{Top}\) and \(\texttt{isEmptyStack}\) should take an extra integer parameter to identify which stack will be used.

You are asked to design an efficient method for keeping 3 stacks within a single linear array so that none of the three stacks overflows until all of memory is used.

1. Give the declaration of the type \(\texttt{threeStacks}\).
2. Write usual stack functions (\(\texttt{CreateStack}\), \(\texttt{Push}\), \(\texttt{Pop}\), \(\texttt{Top}\), \(\texttt{isEmptyStack}\) , \(\texttt{isFullStack}\)) to manipulate the three stacks.
3. Without performing any calculations, give the worst case time complexity of your functions. Justify your answer.

typedef int  element;
typedef struct  {
	element data[N]; 
	int top1,top2;
	int top3, bottom3;
} stack;


stack CreateStack()
{
    stack s;
    s.top1=-1;
    s.top2=N;
    s.top3 = N/2;
    s.bottom3 = N/2 + 1;
    return s;
}

int isEmptyStack(stack p, int n)
{
    if(n==1)
        return p.top1==-1;
    if(n==2)
        return p.top2==N;
    return p.top3 < p.bottom3;
}

int isFullStack(stack p)
{
    return p.top1+1 == p.bottom3 && p.top3+1 == p.top2;
}


int Pop(stack *p, int n)
{
    if(isEmptyStack(*p,n))
        return 0;
    if(n==1)
        p->top1--;
    else
        if(n==2)
            p->top2++;
        else
            p->top3--;
    return 1;
}

int Top(stack p, element *e, int n)
{
    if(isEmptyStack(p,n))
            return 0;
    if(n==1)
        *e=p.data[p.top1];
    else
        if(n==2)
            *e=p.data[p.top2];
        else
            *e=p.data[p.top3];
    return 1;
}


int Push(stack *p, element e, int n)
{
    int empty,i ;
    if(isFullStack(*p))
        return 0;
    if(n==1)
    {
        if(p->top1+1 == p->bottom3) // try to shift S3
        {
            //get the rightmost empty cells
            empty = p->top2 - p->top3-1; 
            for(i=p->top3; i>=p->bottom3;i--)
            {
                p->data[i+empty/2+1] =  p->data[i];
            }
            p->top3 = p->top3+empty/2+1;
            p->bottom3= p->bottom3+empty/2+1;
        }
        p->data[++p->top1] = e;
    }
    else
    {
        if(p->top2 - 1 == p->top3) // try to shift
        {
            //get the leftmost empty cells
            empty = p->bottom3 - p->top1 - 1;
            for(i=p->bottom3; i<=p->top3 ; i++)
            {
                p->data[i-empty/2-1] = p->data[i];
            }
            p->top3 = p->top3 - empty/2 - 1;
            p->bottom3= p->bottom3 - empty/2 - 1;
        }
        if(n==2)
            p->data[--p->top2]=e;
        else
            if(n==3)
                p->data[++p->top3]=e;
    }
    return 1;
}