The input to your program will be a string of letters which symbolize the nodes of a binary tree. The order of appearance of the letters is the pre-order traversal of the tree. A 0(zero) in the string specifies that the relevant child is null. Your program should then accept two letters as input and give as output the path from the first to the second.

Example:
The input to your program will be of the form:

1

ABDF000E00C0G00
DG

the sample tree for this example string is as below

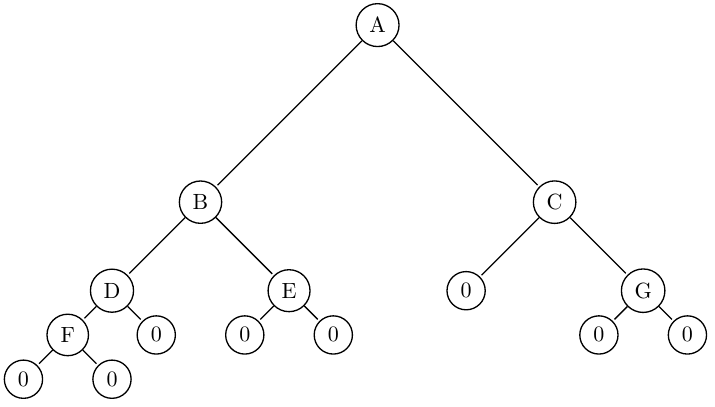
the output for this problem should be:
DBACG

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#define N 1000
typedef char element;



 
 typedef struct Tree Tree;


struct Tree 
{
  Tree * left, * right;
  char element;
};


typedef Tree *Btree;


/*
typedef Tree element;

typedef struct {
	element data[N];
	int top;
} stack;

stack CreateStack()
{
	stack p;
	p.top = -1;
	return p;
}

int isEmptyStack(stack p)
{
	return (p.top == -1);
}

int isFullStack(stack p)
{
	return (p.top == N - 1);
}

int Push(stack *p, element e)
{
	if (isFullStack(*p)) return 0;
	p->data[++p->top] = e;
	return 1;
}

int Pop(stack *p)
{
	if (isEmptyStack(*p)) return 0;
	p->top--;
	return 1;
}

int Top(stack p, element *e)
{
	if (isEmptyStack(p)) return 0;
	*e = p.data[p.top];
	return 1;
}

 
*/
Btree Build(char preorder[], int *start)
{
    Btree B;
    if(preorder[*start]!='\0')
    {
        B=(Btree)malloc(sizeof(Tree));
        B->element = preorder[*start];
        if(B->element=='0')
            B->left=B->right=NULL;
        else
        {
            ++(*start);
            B->left=Build(preorder,start);
            ++(*start);
            B->right=Build(preorder,start);
        }
        return B;
    }
    return NULL;
}




 
Tree *make_empty(Tree *t)
{
  if (t != NULL)
  {
    make_empty(t->left);
    make_empty(t->right);
    free(t);
  }

  return NULL;
}

Tree *find_min(Tree *t)
{
  if (t == NULL)
  {
    return NULL;
  }
  else if (t->left == NULL)
  {
    return t;
  }
  else
  {
    return find_min(t->left);
  }
}

Tree *find_max(Tree *t)
{
  if (t == NULL)
  {
    return NULL;
  }
  else if (t->right == NULL)
  {
    return t;
  }
  else
  {
    return find_max(t->right);
  }
}

Tree *find(int elem, Tree *t)
{
  if (t == NULL)
  {
    return NULL;
  }

  if (elem < t->element)
  {
    return find(elem, t->left);
  }
  else if (elem > t->element)
  {
    return find(elem, t->right);
  }
  else
  {
    return t;
  }
}

//Insert i into the tree t, duplicate will be discarded
//Return a pointer to the resulting tree.                 
Tree * insert(int value, Tree * t) 
{
  Tree * new_node;
    
  if (t == NULL) 
  {
    new_node = (Tree *) malloc (sizeof (Tree));
    if (new_node == NULL) 
    {
	    return t;
    }

    new_node->element = value;

	  new_node->left = new_node->right = NULL;
	  return new_node;
  }
  
  if (value < t->element) 
  {
    t->left = insert(value, t->left);
  } 
  else if (value > t->element) 
  {
	  t->right = insert(value, t->right);
  } 
  else 
  { 
    //duplicate, ignore it
	  return t;
  }
  return t;
}

Tree * delete(int value, Tree * t) 
{
  //Deletes node from the tree
  // Return a pointer to the resulting tree
  Tree * x;
  Tree *tmp_cell;
  
  if (t==NULL) return NULL;
  
  if (value < t->element) 
  {
    t->left = delete(value, t->left);
  } 
  else if (value > t->element) 
  {
	  t->right = delete(value, t->right);
  } 
  else if (t->left && t->right)
  {
    tmp_cell = find_min(t->right);
    t->element = tmp_cell->element;
    t->right = delete(t->element, t->right);
  }
  else
  { 
    tmp_cell = t;
    if (t->left == NULL)
      t = t->right;
    else if (t->right == NULL)
      t = t->left;
    free(tmp_cell);
  }

  return t;
}


//printing tree in ascii

typedef struct asciinode_struct asciinode;

struct asciinode_struct
{
  asciinode * left, * right;

  //length of the edge from this node to its children
  int edge_length; 
    
  int height;      

  int lablen;

  //-1=I am left, 0=I am root, 1=right   
  int parent_dir;   
                         
  //max supported unit32 in dec, 10 digits max
  char label[11];  
};


#define MAX_HEIGHT 1000
int lprofile[MAX_HEIGHT];
int rprofile[MAX_HEIGHT];
#define INFINITY (1<<20)

//adjust gap between left and right nodes
int gap = 3;  

//used for printing next node in the same level, 
//this is the x coordinate of the next char printed
int print_next;    

int MIN (int X, int Y)  
{
  return ((X) < (Y)) ? (X) : (Y);
}

int MAX (int X, int Y)  
{
  return ((X) > (Y)) ? (X) : (Y);
}

asciinode * build_ascii_tree_recursive(Tree * t) 
{
  asciinode * node;
  
  if (t == NULL) return NULL;

  node = malloc(sizeof(asciinode));
  node->left = build_ascii_tree_recursive(t->left);
  node->right = build_ascii_tree_recursive(t->right);
  
  if (node->left != NULL) 
  {
    node->left->parent_dir = -1;
  }

  if (node->right != NULL) 
  {
    node->right->parent_dir = 1;
  }

  sprintf(node->label, "%c", t->element);
  node->lablen = strlen(node->label);

  return node;
}


//Copy the tree into the ascii node structre
asciinode * build_ascii_tree(Tree * t) 
{
  asciinode *node;
  if (t == NULL) return NULL;
  node = build_ascii_tree_recursive(t);
  node->parent_dir = 0;
  return node;
}

//Free all the nodes of the given tree
void free_ascii_tree(asciinode *node) 
{
  if (node == NULL) return;
  free_ascii_tree(node->left);
  free_ascii_tree(node->right);
  free(node);
}

//The following function fills in the lprofile array for the given tree.
//It assumes that the center of the label of the root of this tree
//is located at a position (x,y).  It assumes that the edge_length
//fields have been computed for this tree.
void compute_lprofile(asciinode *node, int x, int y) 
{
  int i, isleft;
  if (node == NULL) return;
  isleft = (node->parent_dir == -1);
  lprofile[y] = MIN(lprofile[y], x-((node->lablen-isleft)/2));
  if (node->left != NULL) 
  {
	  for (i=1; i <= node->edge_length && y+i < MAX_HEIGHT; i++) 
    {
	    lprofile[y+i] = MIN(lprofile[y+i], x-i);
    }
  }
  compute_lprofile(node->left, x-node->edge_length-1, y+node->edge_length+1);
  compute_lprofile(node->right, x+node->edge_length+1, y+node->edge_length+1);
}

void compute_rprofile(asciinode *node, int x, int y) 
{
  int i, notleft;
  if (node == NULL) return;
  notleft = (node->parent_dir != -1);
  rprofile[y] = MAX(rprofile[y], x+((node->lablen-notleft)/2));
  if (node->right != NULL) 
  {
	  for (i=1; i <= node->edge_length && y+i < MAX_HEIGHT; i++) 
    {
	    rprofile[y+i] = MAX(rprofile[y+i], x+i);
    }
  }
  compute_rprofile(node->left, x-node->edge_length-1, y+node->edge_length+1);
  compute_rprofile(node->right, x+node->edge_length+1, y+node->edge_length+1);
}

//This function fills in the edge_length and 
//height fields of the specified tree
void compute_edge_lengths(asciinode *node) 
{
  int h, hmin, i, delta;
  if (node == NULL) return;
  compute_edge_lengths(node->left);
  compute_edge_lengths(node->right);

  /* first fill in the edge_length of node */
  if (node->right == NULL && node->left == NULL) 
  {
	  node->edge_length = 0;
  } 
  else 
  {
    if (node->left != NULL) 
    {
	    for (i=0; i<node->left->height && i < MAX_HEIGHT; i++) 
      {
		    rprofile[i] = -INFINITY;
	    }
	    compute_rprofile(node->left, 0, 0);
	    hmin = node->left->height;
    } 
    else 
    {
	    hmin = 0;
    }
	  if (node->right != NULL) 
    {
	    for (i=0; i<node->right->height && i < MAX_HEIGHT; i++) 
      {
		    lprofile[i] = INFINITY;
	    }
	    compute_lprofile(node->right, 0, 0);
	    hmin = MIN(node->right->height, hmin);
    } 
    else 
    {
	    hmin = 0;
    }
	  delta = 4;
	  for (i=0; i<hmin; i++) 
    {
	    delta = MAX(delta, gap + 1 + rprofile[i] - lprofile[i]);
    }
	  
    //If the node has two children of height 1, then we allow the
    //two leaves to be within 1, instead of 2 
	  if (((node->left != NULL && node->left->height == 1) ||
	      (node->right != NULL && node->right->height == 1))&&delta>4) 
    {
      delta--;
    }
	    
    node->edge_length = ((delta+1)/2) - 1;
  }

  //now fill in the height of node
  h = 1;
  if (node->left != NULL) 
  {
	  h = MAX(node->left->height + node->edge_length + 1, h);
  }
  if (node->right != NULL) 
  {
	  h = MAX(node->right->height + node->edge_length + 1, h);
  }
  node->height = h;
}

//This function prints the given level of the given tree, assuming
//that the node has the given x cordinate.
void print_level(asciinode *node, int x, int level) 
{
  int i, isleft;
  if (node == NULL) return;
  isleft = (node->parent_dir == -1);
  if (level == 0) 
  {
	  for (i=0; i<(x-print_next-((node->lablen-isleft)/2)); i++) 
    {
	    printf(" ");
    }
	  print_next += i;
	  printf("%s", node->label);
	  print_next += node->lablen;
  } 
  else if (node->edge_length >= level) 
  {
	  if (node->left != NULL) 
    {
	    for (i=0; i<(x-print_next-(level)); i++) 
      {
		    printf(" ");
	    }
	    print_next += i;
	    printf("/");
	    print_next++;
    }
	  if (node->right != NULL) 
    {
	    for (i=0; i<(x-print_next+(level)); i++) 
      {
		    printf(" ");
	    }
	    print_next += i;
	    printf("\\");
	    print_next++;
    }
  } 
  else 
  {
	  print_level(node->left, 
                x-node->edge_length-1, 
                level-node->edge_length-1);
	  print_level(node->right, 
                x+node->edge_length+1, 
                level-node->edge_length-1);
  }
}

//prints ascii tree for given Tree structure
void print_ascii_tree(Tree * t) 
{
  asciinode *proot;
  int xmin, i;
  if (t == NULL) return;
  proot = build_ascii_tree(t);
  compute_edge_lengths(proot);
  for (i=0; i<proot->height && i < MAX_HEIGHT; i++) 
  {
	  lprofile[i] = INFINITY;
  }
  compute_lprofile(proot, 0, 0);
  xmin = 0;
  for (i = 0; i < proot->height && i < MAX_HEIGHT; i++) 
  {
	  xmin = MIN(xmin, lprofile[i]);
  }
  for (i = 0; i < proot->height; i++) 
  {
	  print_next = 0;
	  print_level(proot, -xmin, i);
	  printf("\n");
  }
  if (proot->height >= MAX_HEIGHT) 
  {
	  printf("(This tree is taller than %d, and may be drawn incorrectly.)\n", MAX_HEIGHT);
  }
  free_ascii_tree(proot); 
}

 
// find the nodes in the tree
Btree findt(Btree B, element e)
{
    Btree l , r;
    if(!B) return NULL;
    if(B->element == e) return B;
    l= findt(B->left, e);
    r = findt(B->right, e);
    return (l?l:r);
}


// lca
Btree lca(Btree B, Btree l, Btree r)
{
    Btree rl, rr;
    if(!B) return NULL;
    if(B==l || B==r) return B;
    rl=lca(B->left,l,r);
    rr=lca(B->right,l,r);
    if(rl && rr)
        return B;
    else
        return (rl?rl:rr);
    
}


int printPathup(Btree root, Btree dest)
{
    int l , r ;
    if(!root) return 0;
    l = printPathup(root->left, dest);
    r = printPathup(root->right, dest);
    if(root->element == dest->element || l || r)
    {
        printf("%c",root->element);
        return 1;
    }
    return 0;
}


void printPathdown(Btree root, Btree dest, char path[], int size)
{
    if(!root) return;
    path[size]=root->element;
    ++size;
    printPathdown(root->left, dest, path,size);
    printPathdown(root->right, dest, path,size);
    if(root->element == dest->element)
    {
        path[size]='\0';
        printf("%s\n",path+1);
        return;
    }
}


	
	
int main()
{
	int tests, size, i , sizepath;
	char str[N], str2[N], path[N];
	Btree B , Root , left , right;
    int start;

	// read nb of tests
	scanf("%d", &tests);

	// each line: a postfix expression 
	while (tests--)
	{
	    B=NULL;
		scanf("%s", str);
		start=0;
		sizepath=0;
		B=Build(str,&start);
		//printf("\n\n");
		//print_ascii_tree(B);
		scanf("%s",str2);
        left=findt(B, str2[0]);
        right=findt(B, str2[1]);
		Root=lca(B, left ,right );
		//printf("\n\n");
		printPathup(Root,left);
		printPathdown(Root,right,path, sizepath);
		//print from left to root and then from root to right
		//printf("\n\n");
		//print_ascii_tree(Root);
		//printf("%.4f\n", result(B));
	}
	return 0;
}