Pick up sticks is a fascinating game. A collection of colored sticks are dumped in a tangled heap on the table. Players take turns trying to pick up a single stick at a time without moving any of the other sticks. It is very difficult to pick up a stick if there is another stick lying on top of it.
The players therefore try to pick up the sticks in an order such that they never have to pick up a stick from underneath another stick.

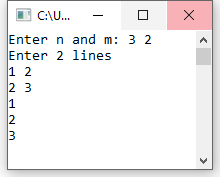
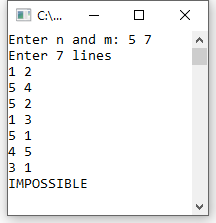
The input is as follows:

• A number \( N \), \( 1 \leq N \leq 1000000 \), indicating the number of sticks. The sticks are numbered
  from 1 to \( N \).
• A number \( M \), \( 1 \leq M \leq 1000000 \) of lines. Each of these lines contains a pair of integers \( a \), \( b \), indicating that there is a point where stick \( a \) lies on top of stick \( b \).
  
  

As output, print \( N \) lines of integers, listing the sticks in the order in which they could be picked up without ever picking up a stick with another stick on top of it. If there are multiple such correct orders, any one will do. If there is no such correct order, output a single line containing the word "\(\texttt{IMPOSSIBLE}\)".

****************************************************
****************************************************

		USING ADJACENCY MATRIX

****************************************************
****************************************************

#include<stdio.h>
#include<stdlib.h>
#define N 20

typedef int element;

typedef struct 
{
	element data[N]; /* queue content */
	int front, length;
} queue;

 


queue CreateQueue()
{
	queue q;
	q.front = 0; q.length=0;
	return q;
}
int isEmptyQueue(queue q)
{
	return q.length == 0;
}

int isFullQueue(queue q)
{
	return q.length ==N;
}

int EnQueue(queue *q, element e)
{
	if (isFullQueue(*q)) return 0;
	q->data[(q->front + q->length)%N] = e;
	q->length = q->length + 1;
	return 1;
}

int DeQueue(queue *q)
{
	if (isEmptyQueue(*q)) return 0;
	q->front=(q->front + 1) % N;
	q->length--;
	return 1;
}

int Front(queue q, element *e)
{
	if (isEmptyQueue(q)) return 0;
	*e = q.data[q.front];
	return 1;
}


typedef struct {
	int V;
	int E;
	int **Adj; // since we need 2 dimensional matrix
} Graph;

Graph* adjacencyMatrix() {
	int i, u, v;
	Graph* G=(Graph*) malloc(sizeof(Graph));
	printf("Enter n and m: ");
	scanf("%d %d", &G->V, &G->E );
	G->Adj = (int **)malloc((G->V+1) * sizeof(int*));
	for (u = 1; u <= G->V; u++)
		G->Adj[u] = (int *)malloc((G->V + 1) * sizeof(int));

	for (u = 1; u<=G->V; u++)
		for (v = 1; v<=G->V; v++)
			G->Adj[u][v] = 0;
	printf("Enter %d lines\n", G->E);
	for (i = 1; i <= G->E; i++) {
		scanf("%d %d", &u,&v);
		G->Adj[u][v] = 1;
	}
	return G;
}
 

void topologicalSort(Graph *G) {
	queue q, topologicalorder;
	int counter;
	int v, w;
	int *indegree;
 
	indegree= (int *)malloc((G->V + 1) * sizeof(int));
	for (v = 1; v <= G->V; v++)
		indegree[v] = 0;

	for (v = 1; v <= G->V; v++)
		for (w = 1; w <= G->V; w++)
			if (G->Adj[v][w] == 1)
				indegree[w]++;
 
       
	q = CreateQueue();
	topologicalorder = CreateQueue();

	counter = 0;
	for (v = 1; v <= G->V; v++)
		if (indegree[v]==0)
			EnQueue(&q, v);
	while (Front(q,&v)) {
		DeQueue(&q);
		++counter;
		EnQueue(&topologicalorder,v );
		for (w = 1; w <= G->V; w++)
			if (G->Adj[v][w] == 1)
				if(--indegree[w] == 0)
					EnQueue(&q, w);

	}
	if (counter != G->V)
		printf("IMPOSSIBLE");
	else
		while (Front(topologicalorder, &v) && DeQueue(&topologicalorder))
			printf("%d\n", v);
}
 

void test() {
	int u, v;
	Graph *G = adjacencyMatrix();
	topologicalSort(G);
}


int main()
{
	test();
	return 0;
}




****************************************************
****************************************************

		USING ADJACENCY LIST

****************************************************
****************************************************



#include<stdio.h>
#include<stdlib.h>
#define N 20

typedef int element;

typedef struct 
{
	element data[N]; /* queue content */
	int front, length;
} queue;


typedef struct node {
	int vertexNumber;
	struct node * next;
} node;
typedef struct {
	int V;
	int E;
	node** Adj;  //array of linked list
} Graph;




queue CreateQueue()
{
	queue q;
	q.front = 0; q.length=0;
	return q;
}
int isEmptyQueue(queue q)
{
	return q.length == 0;
}

int isFullQueue(queue q)
{
	return q.length ==N;
}

int EnQueue(queue *q, element e)
{
	if (isFullQueue(*q)) return 0;
	q->data[(q->front + q->length)%N] = e;
	q->length = q->length + 1;
	return 1;
}

int DeQueue(queue *q)
{
	if (isEmptyQueue(*q)) return 0;
	q->front=(q->front + 1) % N;
	q->length--;
	return 1;
}

int Front(queue q, element *e)
{
	if (isEmptyQueue(q)) return 0;
	*e = q.data[q.front];
	return 1;
}

 




Graph* adjacencyList() {
	int i, x, y;
	node * temp, *temp2;
	Graph* G=(Graph*) malloc(sizeof(Graph));

	printf("Enter n and m: ");
	scanf("%d %d", &G->V, &G->E );
	G->Adj = (node **)malloc((G->V+1) * sizeof(node));
	for (i = 1; i <= G->V; i++) {
		G->Adj[i] = (node *)malloc(G->V * sizeof(node));
		G->Adj[i]->vertexNumber = i;
		G->Adj[i]->next = NULL;
	}
 
	printf("Enter %d lines\n", G->E);
	for (i = 1; i <= G->E; i++) {
		scanf("%d %d", &x,&y);
		temp = (node*)malloc(sizeof(node));
		temp->vertexNumber = y;
        	temp->next = NULL;
        
		temp2 = G->Adj[x];
		while (temp2->next != NULL)
			temp2 = temp2->next;
		temp2->next = temp;
		
	}
	return G;
}

 

void topologicalSort(Graph *G) {
	queue q, topologicalorder;
	int counter;
	int v, w;
	int *indegree;
	node * head;


	indegree= (int *)malloc((G->V + 1) * sizeof(int));
	for (v = 1; v <= G->V; v++)
		indegree[v] = 0;

 
	for (v = 1; v <= G->V; v++)
	{
		head=G->Adj[v]->next;
		while(head)
		{
			indegree[head->vertexNumber]++;
			head=head->next;
		}
	}
       
	q = CreateQueue();
	topologicalorder = CreateQueue();
 
	counter = 0;
	for (v = 1; v <= G->V; v++)
		if (indegree[v]==0)
			EnQueue(&q, v);

	while (Front(q,&v)) {
		DeQueue(&q);
		++counter;
		EnQueue(&topologicalorder,v );
		head=G->Adj[v]->next;
		while(head)
		{
			if(--indegree[head->vertexNumber] == 0)
				EnQueue(&q, head->vertexNumber);
			head=head->next;
		}

	}
	if (counter != G->V)
		printf("IMPOSSIBLE");

	while (Front(topologicalorder, &v) && DeQueue(&topologicalorder))
			printf("%d\n", v);
}



void test() {
	Graph *G = adjacencyList();
	topologicalSort(G);
}

int main()
{
	test();
	return 0;
}