A minimum spanning tree of an undirected graph \(G\) is a tree formed from graph edges that connect all the vertices of \(G\) with minimum total cost (weights). A minimum spanning tree exists only if the graph is connected.
Prim's algorithm is almost the same as Dijkstra's algorithm. As in Dijkstra's algorithm, in Prim's algorithm we keep the values distance and paths in the distance table. The only exception is that since the definition of distance is different, the updating statement also changes a little. The update statement is simpler than before.
Example:
Prim's algorithm can be used to find the Minimal Spanning Tree of the graph.
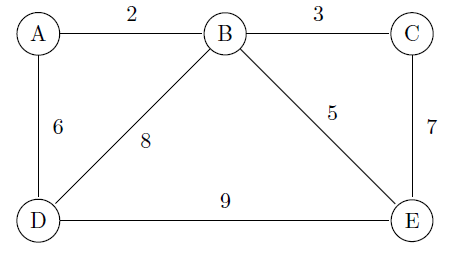
The Minimal Spanning Tree which Prim's algorithm generates is:
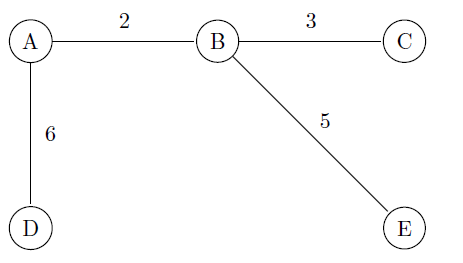
Given the following declaration,typedef struct { int V; int E; int **Adj; } Graph;
Write a function that reads an undirected weighted graph.- Write a function that takes as parameters an undirected weighted graph and an vertex, and returns the final Minimal Spanning Tree using Prim's algorithm.
- Write a main function to test your function.

Difficulty level

Video recording
This exercise is mostly suitable for students
****************************************************
****************************************************
USING PRIORITY QUEUE V1
****************************************************
****************************************************
#include<stdio.h>
#include<stdlib.h>
#define N 20
typedef struct
{
int u, v, w;
} edge;
typedef edge element;
struct cell {
element data;
int priority;
struct cell *next;
};
typedef struct {
struct cell *front;
} queue;
typedef struct {
int V;
int E;
int **Adj; // since we need 2 dimensional matrix
} Graph;
queue CreateQueue()
{
queue q;
q.front = NULL;
return q;
}
int isEmptyQueue(queue q)
{
return q.front == NULL;
}
int EnQueue(queue *q, element e, int priority)
{
struct cell *temp, *href;
temp = (struct cell *) malloc(sizeof(struct cell));
if (!temp) return 0;
temp->data = e;
temp->priority = priority;
if (q->front == NULL || priority < q->front->priority) {/*Queue is empty or item to be added has priority more than first item*/
temp->next = q->front;
q->front = temp;
}
else
{
href = q->front;
while (href->next != NULL && href->next->priority <= priority)
href = href->next;
temp->next = href->next;
href->next = temp;
}
return 1;
}
int DeQueue(queue *q)
{
struct cell *temp;
if (isEmptyQueue(*q)) return 0;
temp = q->front;
q->front = q->front->next;
free(temp);
return 1;
}
int Front(queue q, element *e)
{
if (isEmptyQueue(q)) return 0;
*e = q.front->data;
return 1;
}
void display_queue(queue tmp)
{
struct cell *temp = tmp.front;
if (temp == NULL)
printf("Queue is empty\n");
else
{
printf("Queue is :\n");
printf("Item\n");
while (temp != NULL)
{
printf("w=%5d u=%5d v=%5d\n\n", temp->priority, temp->data.u, temp->data.v);
temp = temp->next;
}
}
}
Graph* adjacencyMatrix() {
int i, u, v, w;
Graph* G = (Graph*)malloc(sizeof(Graph));
printf("Enter the number of Vertices: ");
scanf("%d", &G->V);
printf("Enter the number of Edges: ");
scanf("%d", &G->E);
G->Adj = (int **)malloc(G->V * sizeof(int*));
for (u = 0; u < G->V; u++)
G->Adj[u] = (int *)malloc(G->V * sizeof(int));
for (u = 0; u<G->V; u++)
for (v = 0; v<G->V; v++)
G->Adj[u][v] = 0;
for (i = 0; i < G->E; i++) {
printf("Enter the edge and the weight: ");
scanf("%d %d %d", &u, &v, &w);
G->Adj[u][v] = w;
G->Adj[v][u] = w;
}
return G;
}
void Prim(Graph *G, int s) {
int i,j, k;
int *U;
element *T, v ;
queue q;
U = (int *)malloc(G->V * sizeof(int));
T = (element *)malloc((G->V - 1 ) * sizeof(element));
q = CreateQueue();
for (i = 0; i<G->V; i++)
U[i]=0;
U[s]=1;
for (j = 0; j<G->V; j++)
if(G->Adj[s][j])
EnQueue(&q, (element){s,j,G->Adj[s][j]}, G->Adj[s][j]);
j=0;
for (i = 0; i<G->V - 1; i++)
{
while(Front(q,&v) && DeQueue(&q) )
{
for (k = 0; k<G->V; k++)
if(G->Adj[v.v][k] && !U[k] )
EnQueue(&q, (element){v.v,k,G->Adj[v.v][k]}, G->Adj[v.v][k]);
if(U[v.u] && !U[v.v])
{
U[v.v]=1;
T[j++]=v;
break;
}
}
}
for (i = 0; i<G->V - 1; i++)
printf("Edge: %d - %d Weight %d\n", T[i].u, T[i].v , T[i].w);
}
void test() {
int u, v;
Graph *G = adjacencyMatrix();
Prim(G, 3);
}
int main()
{
test();
return 0;
}
****************************************************
****************************************************
USING PRIORITY QUEUE V2
WORKS WHEN STARTING WITH
VERTEX WITH SMALLEST EDGE VALUE
****************************************************
****************************************************
#include<stdio.h>
#include<stdlib.h>
#define N 20
typedef struct
{
int u, v, w;
} edge;
typedef edge element;
struct cell {
element data;
int priority;
struct cell *next;
};
typedef struct {
struct cell *front;
} queue;
typedef struct {
int V;
int E;
int **Adj; // since we need 2 dimensional matrix
} Graph;
queue CreateQueue()
{
queue q;
q.front = NULL;
return q;
}
int isEmptyQueue(queue q)
{
return q.front == NULL;
}
int EnQueue(queue *q, element e, int priority)
{
struct cell *temp, *href;
temp = (struct cell *) malloc(sizeof(struct cell));
if (!temp) return 0;
temp->data = e;
temp->priority = priority;
if (q->front == NULL || priority < q->front->priority) {/*Queue is empty or item to be added has priority more than first item*/
temp->next = q->front;
q->front = temp;
}
else
{
href = q->front;
while (href->next != NULL && href->next->priority <= priority)
href = href->next;
temp->next = href->next;
href->next = temp;
}
return 1;
}
int DeQueue(queue *q)
{
struct cell *temp;
if (isEmptyQueue(*q)) return 0;
temp = q->front;
q->front = q->front->next;
free(temp);
return 1;
}
int Front(queue q, element *e)
{
if (isEmptyQueue(q)) return 0;
*e = q.front->data;
return 1;
}
void display_queue(queue tmp)
{
struct cell *temp = tmp.front;
if (temp == NULL)
printf("Queue is empty\n");
else
{
printf("Queue is :\n");
printf("Item\n");
while (temp != NULL)
{
printf("w=%5d u=%5d v=%5d\n\n", temp->priority, temp->data.u, temp->data.v);
temp = temp->next;
}
}
}
Graph* adjacencyMatrix() {
int i, u, v, w;
Graph* G = (Graph*)malloc(sizeof(Graph));
printf("Enter the number of Vertices: ");
scanf("%d", &G->V);
printf("Enter the number of Edges: ");
scanf("%d", &G->E);
G->Adj = (int **)malloc(G->V * sizeof(int*));
for (u = 0; u < G->V; u++)
G->Adj[u] = (int *)malloc(G->V * sizeof(int));
for (u = 0; u<G->V; u++)
for (v = 0; v<G->V; v++)
G->Adj[u][v] = 0;
for (i = 0; i < G->E; i++) {
printf("Enter the edge and the weight: ");
scanf("%d %d %d", &u, &v, &w);
G->Adj[u][v] = w;
G->Adj[v][u] = w;
}
return G;
}
void Prim(Graph *G, int s) {
int i,j;
int *U;
element *T, v ;
queue q;
U = (int *)malloc(G->V * sizeof(int));
T = (element *)malloc((G->V - 1 ) * sizeof(element));
q = CreateQueue();
for (i = 0; i<G->V; i++)
{
U[i]=0;
for (j = 0; j<G->V; j++)
if(G->Adj[i][j])
EnQueue(&q, (element){i,j,G->Adj[i][j]}, G->Adj[i][j]);
}
U[s]=1;
j=0;
for (i = 0; i<G->V - 1; i++)
{
while(Front(q,&v) && DeQueue(&q))
if(U[v.u] && !U[v.v])
{
U[v.v]=1;
T[j++]=v;
break;
}
}
for (i = 0; i<G->V - 1; i++)
printf("Edge: %d - %d Weight %d\n", T[i].u, T[i].v , T[i].w);
}
void test() {
int u, v;
Graph *G = adjacencyMatrix();
Prim(G, 0);
}
int main()
{
test();
return 0;
}Back to the list of exercises
Looking for a more challenging exercise, try this one !!
 Sorting using the counting sort algorithm
Sorting using the counting sort algorithm