A Binary Search Tree (BST) of whole integers can be represented by an array where the root is located at 0 and the contents of the remaining nodes correspond to the course in width of the tree. i.e. every node has two locations for its left and right children. In the case where one (or both) of the two children doesn't exist, the corresponding location will contain the value -1.

Ex : The array

$\begin{array}{|c|c|c|c|c|c|c|}\hline 6 & 4 & 8 & 2 & 5 & -1 & 10 \\ \hline \end{array}$

corresponds to the tree

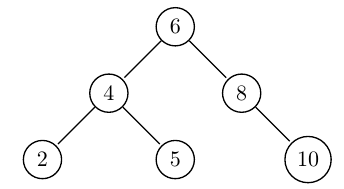
• Write the corresponding declaration.
• Write a function that inserts a natural integer in a BST.
• Write a function that calculates the number of nodes having only one child in a BST.
• Write a function that tests if a BT is a Binary Search Tree.

typedef int element;
 
typedef struct{
    int element[M];
    int size;
} BST;

int insert_h(BST *B, int index, element e)
{
    if(index>=M) return 0;
    if(B->element[index]==-1)
    {
        B->element[index]=e;
        B->size =max(B->size,index+1);
        return 1;
    }
    if(e==B->element[index])
        return 0;
    if(e<B->element[index])
        return insert_h(B, 2*index+1, e);
    return insert_h(B, 2*index +2, e);
    
}

int  insert(BST *B, element e)
{
    return insert_h(B,0 ,e);
}

int one_child_h(BST B, int i)
{
    if(B.element[i]==-1) return 0;
    if(B.element[2*i+1]!=-1 && B.element[2*i+2]==-1 )
        return 1+ one_child_h(B,2*i+1);
    if(B.element[2*i+1]==-1 && B.element[2*i+2]!=-1 )
        return 1+ one_child_h(B,2*i+2);
    return one_child_h(B,2*i+1) + one_child_h(B,2*i+2);
}

int one_child(BST B)
{
       return one_child_h(B,0);
}


int minT(BST B, int i)
{
    if(B.element[i]==-1) return INT_MAX;
    if(B.element[2*i+1]==-1 && B.element[2*i+2]==-1) return B.element[i];
    return min(B.element[i], min(minT(B,2*i+1), minT(B,2*i+2)));
}

int maxT(BST B, int i)
{
    if(B.element[i]==-1) return INT_MIN;
    if(B.element[2*i+1]==-1 && B.element[2*i+2]==-1) return B.element[i];
    return max(B.element[i], max(maxT(B,2*i+1), maxT(B,2*i+2)));
}

int isBst_h(BST B, int i)
{
    if(B.element[i]==-1 || B.element[2*i+1]==-1 && B.element[2*i+2]==-1 ) return 1;
    if(B.element[i] < maxT(B,2*i+1)) return 0;
    if(B.element[i] > minT(B,2*i+2)) return 0;
    return isBst_h(B,2*i+1 ) && isBst_h(B,2*i+2);
}


int isBst(BST B)
{
    return isBst_h(B,0);
}