• Write a recursive function $\texttt{int max$\_$rec(Btree B, int root$\_$index)}$ that returns the maximum element in a binary tree statically implemented rooted at index $\texttt{root$\_$index}$.
  Example: Consider the following Binary tree and its representation using an array: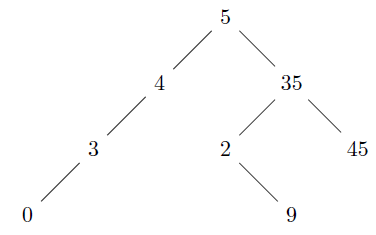
  
  

  $\begin{array}{|c|c|c|c|} \hline\textbf{Index} & \textbf{Root} & \textbf{Left} & \textbf{Right} \\ \hline0 & \textit{Rnd} & \textit{Rnd} & \textit{Rnd} \\ \hline1 & 5 & 2 & 3 \\ \hline2 & 4 & 4 & 0 \\ \hline3 & 35 & 5 & 6 \\ \hline4 & 3 & 7 & 0 \\ \hline5 & 2 & 0 & 8 \\ \hline6 & 45 & 0 & 0 \\ \hline7 & 0 & 0 & 0 \\ \hline8 & 9 & 0 & 0 \\ \hline9 & \textit{Rnd} & -1 & \textit{Rnd} \\ \hline
  \end{array}$

  where Rnd designates a random number.

  • $\texttt{max$\_$rec(B, 1)}$ returns 45;

  • $\texttt{max$\_$rec(B, 2)}$ returns 4 since the maximum element of the tree rooted at element of value 4 ($\texttt{root$\_$index}=2$) is equal to 4;

  • $\texttt{max$\_$rec(B, 5)}$ returns 9.

• Without performing calculation, give the complexity of the above function.

• Write a recursive function $\texttt{int isBST(Btree tree)}$ that checks whether a statically implemented Binary tree is a Binary Search Tree.
  Your function should return 0 for the tree above.

• Write an iterative function that calculates the width of a statically implemented Binary tree.
  Recall that the width of a tree is equal to the maximum of widths of all levels.
  Your function should return 3 for the tree above.

1.	
int max_rec(Btree B, int i)
{
	if(i==0) return INT_MIN;
	if(B.data[i].left_subtree == 0 && B.data[i].right_subtree==0)  
return B.data[i].root;
 
	return max(B.data[i].root,
			max(
					max_rec(B,B.data[i].left_subtree), 
					max_rec(B,B.data[i].right_subtree)
			)
		    );
}

2.	
O(n) where n is the number of nodes in the tree


3.	
int min_rec(Btree B, int i)
{
	if(i==0) return INT_MAX;
	if(B.data[i].left_subtree == 0 && B.data[i].right_subtree==0)  
return B.data[i].root;
 
	return min(B.data[i].root,
			min(
					min_rec(B,B.data[i].left_subtree), 
					min_rec(B,B.data[i].right_subtree)
			)
		    );
}

int isBST(Btree tree)
{
	return isBSTC(tree, tree.root_index);
}



int isBSTC(Btree tree, int i)
{
	 if(i == 0)return 1;
if(tree.data[i].left_subtree && 
max_rec(tree, tree.data[i].left_subtree) > tree.data[i].root)
		 return 0;

	 if(tree.data[i].right_subtree  && 
min_rec(tree, tree.data[i].right_subtree) < tree.data[i].root)
		 return 0;

	 if(!isBSTC(tree, tree.data[i].left_subtree) || 
!isBSTC(tree, tree.data[i].right_subtree)) 
		 return 0;

	 return 1;
 }


4.	
int width(Btree A)
{
    		queue f =CreateQueue();
 		int lcour = 1, lmax = 1, nivcour = 1;
		element1 E,X;

    		if (A.root_index == 0) return 0;
 
    		E.tree = A;
    		E.level = 1;
		E.root=A.root_index ;
		EnQueue(&f,E);
		while(Front(f,&E))
    		{
        		if (E.level == nivcour) lcour++ ;
        		else
       	 	{
            		if (lcour > lmax) lmax = lcour;
            		lcour = 1;
            		nivcour = E.level;
        		}
			DeQueue(&f);

        		if (E.tree.data[E.root].left_subtree!=0) 
			{
				X.tree = E.tree; 
				X.level = E.level+1; 
				X.root=E.tree.data[E.root].left_subtree; 
				EnQueue(&f,X);
			}

			if (E.tree.data[E.root].right_subtree!=0) 	
			{
				X.tree = E.tree;
				X.level = E.level+1; 
				X.root=E.tree.data[E.root].right_subtree; 
				EnQueue(&f,X);
			}
    	}
    	return lmax;
}