The Stern-Brocot tree is an elegant construction to represent the set of all positive fractions. It was independently discovered by German mathematician Moritz Stern in 1858 and by French watchmaker Achille Brocot in 1861.

The construction starts at the zeroth iteration with the two fractions \[\frac{0}{1}, \frac{1}{0}\].

At every subsequent iteration, consider all adjacent fractions $\frac{a}{b}$ and $\frac{c}{d}$ and insert their mediant $\frac{a+c}{b+d}$ between them.

The first few iterations look like this:
\[\frac{0}{1}, \frac{1}{1}, \frac{1}{0}\]
\[\frac{0}{1}, \frac{1}{2}, \frac{1}{1}, \frac{2}{1}, \frac{1}{0}\]
\[\frac{0}{1}, \frac{1}{3}, \frac{1}{2}, \frac{2}{3}, \frac{1}{1}, \frac{3}{2}, \frac{2}{1}, \frac{3}{1}, \frac{1}{0}\]

Continuing this process to infinity this covers all positive fractions. Additionally, all fractions will be unique and irreducible.

Besides the list representation, in the Stern-Brocot tree representation shown on the next page, every fraction has two children. Each child is the mediant of the closest ancestor on the left and the closest ancestor to the right.

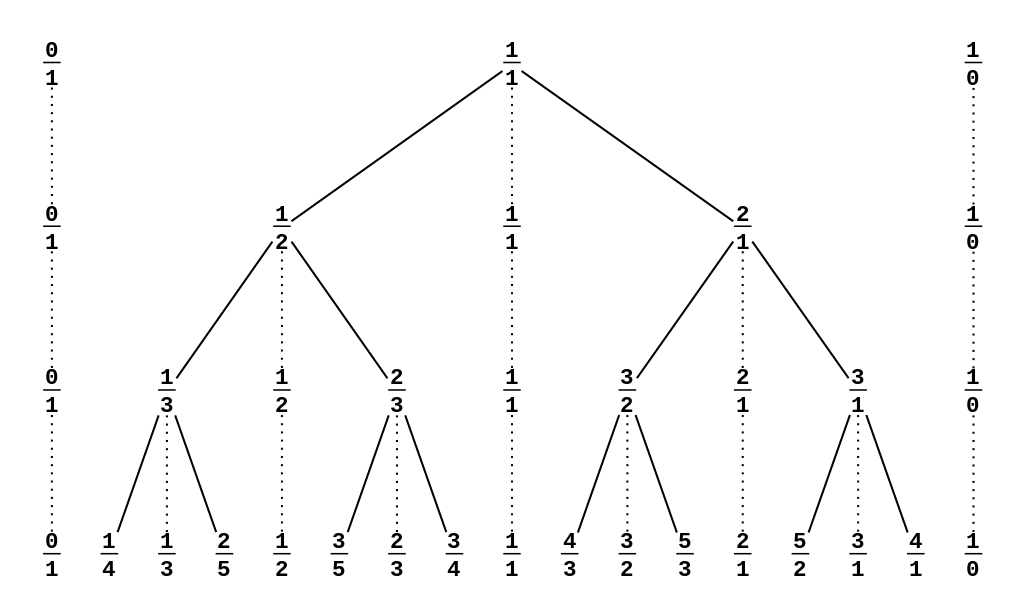
• Give all the declaration needed to declare such a tree.
• Write a recursive function that, given a height $h$, creates and returns a Stern-Brocot tree of height $h$.
• Without writing any code, give the output of the inorder traversal of the above Stern-Brocot tree.
• Write a function that, given a Stern-Brocot tree and an irreducible fraction $f$, returns a pointer to $f$ in the tree. 

The simplicity of a fraction is a property introduced by Pierre Lamothe whose research focuses on music and harmony. He associated with any irreducible fraction $\frac{p}{q}$ the number $\frac{1}{pq}$, called its simplicity. The sum of simplicities of all fractions in any level of the Stern-Brocot tree equals 1.

• Write an iterative function that, given a Stern-Brocot tree, performs the level-order traversal and checks whether the sum of simplicities of all fractions in any level equals 1.

The Farey sequence of order $n$ is the sorted sequence of fractions in the closed interval $[0,1]$ that have denominator less than or equal to $n$. The Farey sequence of order $n$ may be found by an inorder traversal of the left subtree of the Stern-Brocot tree, backtracking whenever a number with denominator greater than $n$ is reached.

• Write an iterative function that, given a Stern-Brocot tree and a number $n$, displays the Farey sequence of order $n$.

** A **

typedef struct{
	int num;
	int denum;
} element;

typedef struct node
{
	element data;
	struct node *left,*right;
} *Btree;


** B **
void CreateSternBrocotTree_h(Btree *B, int a, int b, int c, int d, int height)
{
	int x , y;
	if(height>0)
	{
        	x=a+c;
        	y=b+d;
         	*B=(Btree) malloc(sizeof(struct node));
         	(*B)->data.num=x;
         	(*B)->data.denum=y;
         	CreateSternBrocotTree_h(&((*B)->left), a,  b, x, y, height-1);
         	CreateSternBrocotTree_h(&((*B)->right), x, y, c ,d , height-1);
	}
}

Btree CreateSternBrocotTree(int height)
{
	Btree B=NULL;
	CreateSternBrocotTree_h(&B, 0 , 1, 1, 0, height);
	return B;
}


** C **
1/4 1/3 2/5 1/2 3/5 2/3 3/4 1/1 4/3 3/2 5/3 2/1 5/2 3/1 4/1


** D **
Btree search(Btree B, element e)
{
	double res;
	if(!B) return NULL;
	res = (B->data.num * e.denum -B->data.denum * e.num) / (1.0*e.denum*B->data.denum );
	if(res==0) return B;
	if(res<0) 
		return search(B->right, e);
	return search(B->left, e);
}


** E **
int levelorder(Btree B)
{
	queue q = CreateQueue();
 
	double sum;
	elementq el, tmp;
	int currentlevel;

	if(B==NULL) return 0;

	el.B=B;
	el.level=1;
	EnQueue(&q,el);
	sum=0;
	currentlevel=1;
	while(Front(q,&el))
	{
		DeQueue(&q);
	
		if(currentlevel!=el.level)
		{
			if(sum-1>10E-9) return 0;
		    	sum=0;
		    	currentlevel++; 
		}
		sum+=1.0/(el.B->data.num * el.B->data.denum);
		 
		if(el.B->left != NULL)
		{
		    	tmp.B=el.B->left;
		    	tmp.level = el.level+1;
		    	EnQueue(&q,tmp);
		}
			
		if(el.B->right != NULL)
		{
		    	tmp.B=el.B->right;
		    	tmp.level = el.level+1;
		    	EnQueue(&q,tmp);
		}
	}
	 
	if(sum-1>10E-9) return 0;
	return 1;
}


** F **
void inorderI(Btree B, int n)
{
	Btree S=B;
	stack s=CreateStack();
	int proceed = 1;

	while(proceed)
	{
		while(B != NULL)
		{
			if(B->data.denum>n) 
		        	break;
			Push(&s,B);
			B=B->left;
		}
		if(!isEmptyStack(s) )
		{
			Top(s,&B);
			Pop(&s);
			if(S==B) 
			    proceed = 0;
			printf("%d/%d ",B->data.num, B->data.denum);
			B=B->right;
		}
		else
			proceed=0;
	}
}