Given a Balanced Binary Search Tree and a target sum, write an iterative function that returns $$\texttt{true}$$ if there is a pair with sum equals to target sum, otherwise return $$\texttt{false}$$.

Expected time complexity is $$\texttt{O(n)}$$. Any modification to Binary Search Tree is not allowed. 

Method: traverse $$\texttt{BST}$$ in Normal Inorder and Reverse Inorder simultaneously. In reverse inorder, start from the rightmost node which is the maximum value node. In normal inorder, start from the left most node which is minimum value node. Add sum of current nodes in both traversals and compare this sum with given target sum. If the sum is same as target sum, return $$\texttt{true}$$. If the sum is more than target sum, move to next node in reverse inorder traversal, otherwise move to next node in normal inorder traversal. If any of the traversals is finished without finding a pair, return $$\texttt{false}$$. 

Example: For the following tree,

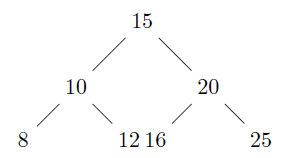
the output should be :

int isPairPresent(Btree root, int target)
{

	stack s1 = CreateStack();
	stack s2 = CreateStack();
 
	int done1 = 0, done2 = 0;
    	int val1 = 0, val2 = 0;
    	Btree curr1 = root, curr2 = root;
 
    	while (1)
    	{
        	while (done1 == 0)
        	{
            		if (curr1 != NULL)
            		{
                		Push(&s1, curr1);
                		curr1 = curr1->left;
            		}
            		else
            		{
				if (isEmptyStack(s1))
                   			done1 = 1;
                		else
                		{
					Top(s1,&curr1);
					Pop(&s1);
					val1 = curr1->data;
                    			curr1 = curr1->right;
                    			done1 = 1;
                		}
            		}
        	}
 
        	while (done2 == 0)
        	{
            		if (curr2 != NULL)
            		{
                		Push(&s2, curr2);
                		curr2 = curr2->right;
            		}
            		else
            		{
                		if (isEmptyStack(s2))
                   			done2 = 1;
                		else
                		{
                    			Top(s2,&curr2); 
					Pop(&s2);
                    			val2 = curr2->data;
                   		 	curr2 = curr2->left;
                    			done2 = 1;
                		}
            		}
        	}
 
        	if ((val1 != val2) && (val1 + val2) == target)
        	{
            		printf("\n Pair Found: %d + %d = %d\n", val1, val2, target);
            		return 1;
        	}
        	else if ((val1 + val2) < target)
            		done1 = 0;
        	else if ((val1 + val2) > target)
            		done2 = 0;
        	if (val1 >= val2)
            		return 0;
    	}
}